

分析 (1)根據等邊三角形的性質可得AC=AD,再根據直角三角形30°角所對的直角邊等于斜邊的一半求出AC=$\frac{1}{2}$AB,然后求出AC=BD,再根據等邊三角形的性質求出點C到AB的距離等于點D到AC的距離,然后根據等底等高的三角形的面積相等解答即可.
(2)根據旋轉的性質可得BC=CE,AC=CD,再求出∠ACN=∠DCM,然后利用“角角邊”證明△ACN和△DCM全等,根據全等三角形對應邊相等可得AN=DM,然后利用等底等高的三角形的面積相等證明;
(3)過點D作DF1∥BE,求出四邊形BEDF1是菱形,根據菱形的對邊相等可得BE=DF1,然后根據等底等高的三角形的面積相等可知點F1為所求的點,過點D作DF2⊥BD,求出∠F1DF2=60°,從而得到△DF1F2是等邊三角形,然后求出DF1=DF2,再求出∠CDF1=∠CDF2,利用“邊角邊”證明△CDF1和△CDF2全等,根據全等三角形的面積相等可得點F2也是所求的點,然后在等腰△BDE中求出BE的長即可.
解答 解:(1))∵∠B=30°,∠C=90°,
∴CD=AC=$\frac{1}{2}$AB,
∴BD=AD=AC,
根據等邊三角形的性質,△ACD的邊AC、AD上的高相等,
∴△BDC的面積和△AEC的面積相等(等底等高的三角形的面積相等),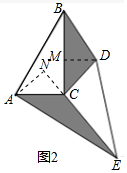
即S1=S2;
故答案為:S1=S2;
(2)如圖,延長EC過點A做AN⊥EC延長線于N,過點D做DM⊥BC于M,
∵△DEC是由△ABC繞點C旋轉得到,
∴BC=CE,AC=CD,
∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°-90°=90°,
∴∠ACN=∠DCM,
∵在△ACN和△DCM中,
$\left\{\begin{array}{l}{∠ACN=∠DCM}\\{∠ANC=∠DMC}\\{AC=DC}\end{array}\right.$,
∴△ACN≌△DCM(AAS),
∴AN=DM,
∴△BDC的面積和△AEC的面積相等(等底等高的三角形的面積相等),
即S1=S2;
(3)如圖,過點D作DF1∥BE,易求四邊形BEDF1是菱形,
所以BE=DF1,且BE、DF1上的高相等,
此時S△DCF1=S△BDE;
過點D作DF2⊥BD,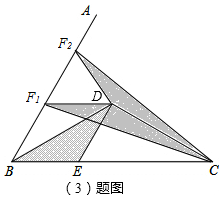
∵∠ABC=60°,F1D∥BE,
∴∠F2F1D=∠ABC=60°,
∵BF1=DF1,∠F1BD=$\frac{1}{2}$∠ABC=30°,∠F2DB=90°,
∴∠F1DF2=∠ABC=60°,
∴△DF1F2是等邊三角形,
∴DF1=DF2,
∵BD=CD,∠ABC=60°,點D是角平分線上一點,
∴∠DBC=∠DCB=$\frac{1}{2}$×60°=30°,
∴∠CDF1=180°-∠BCD=180°-30°=150°,
∠CDF2=360°-150°-60°=150°,
∴∠CDF1=∠CDF2,
∵在△CDF1和△CDF2中,
$\left\{\begin{array}{l}{D{F}_{1}=D{F}_{2}}\\{∠CD{F}_{1}=∠CD{F}_{2}}\\{CD=CD}\end{array}\right.$,
∴△CDF1≌△CDF2(SAS),
∴點F2也是所求的點,
∵∠ABC=60°,點D是角平分線上一點,DE∥AB,
∴∠DBC=∠BDE=∠ABD=$\frac{1}{2}$×60°=30°,
又∵BD=4,
∴BE=$\frac{1}{2}$×4÷cos30°=$\frac{4\sqrt{3}}{3}$,
∴BF1=$\frac{4\sqrt{3}}{3}$,
BF2=BF1+F1F2=$\frac{8\sqrt{3}}{3}$,
故BF的長為$\frac{4\sqrt{3}}{3}$或$\frac{8\sqrt{3}}{3}$.
點評 本題考查了旋轉的性質,三角形的面積,等邊三角形的判定與性質,直角三角形30°角所對的直角邊等于斜邊的一半的性質,熟練掌握等底等高的三角形的面積相等以及旋轉的性質是解題的關鍵.


科目:初中數學 來源: 題型:選擇題
 如圖,AD是△ABC的角平分線,DE、DF分別是△ABD和△ACD的高,則下列說法正確的是( )
如圖,AD是△ABC的角平分線,DE、DF分別是△ABD和△ACD的高,則下列說法正確的是( )| A. | AD垂直FE | B. | AD平分EF | C. | EF垂直平分AD | D. | AD垂直平分EF |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
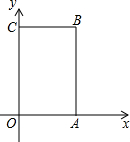 如圖,長方形OABC中,O為直角坐標系的原點,A、C兩點的坐標分別為(2,0)、(0,4).
如圖,長方形OABC中,O為直角坐標系的原點,A、C兩點的坐標分別為(2,0)、(0,4).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系xOy中,一次函數y=ax+b的圖象與反比例函數y=$\frac{k}{x}$的圖象相交于點A(-4,-2),B(m,4),與y軸相交于點C.
如圖,在平面直角坐標系xOy中,一次函數y=ax+b的圖象與反比例函數y=$\frac{k}{x}$的圖象相交于點A(-4,-2),B(m,4),與y軸相交于點C.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
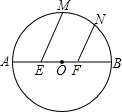 如圖,AB為⊙O的直徑,E、F為AB的三等分點,M、N為$\widehat{AB}$上兩點,且∠MEB=∠NFB=60°,EM+FN=$\sqrt{33}$,則直徑AB的長為6.
如圖,AB為⊙O的直徑,E、F為AB的三等分點,M、N為$\widehat{AB}$上兩點,且∠MEB=∠NFB=60°,EM+FN=$\sqrt{33}$,則直徑AB的長為6.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com