
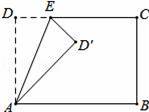
如圖,在矩形ABCD中,AD=5,AB=8,點E為DC邊上的一個動點,把△ADE沿AE折疊,當點D的對應點剛好D落在矩形ABCD的對稱軸上時,則DE的長為 .


 或
或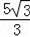
 .
.
【考點】翻折變換(折疊問題).
【分析】過點D′作MN⊥AB于點N,MN交CD于點M,由矩形有兩條對稱軸可知要分兩種情況考慮,根據對稱軸的性質以及折疊的特性可找出各邊的關系,在直角△EMD′與△AND′中,利用勾股定理可得出關于DM長度的一元二次方程,解方程即可得出結論.
【解答】解:過點D′作MN⊥AB于點N,MN交CD于點M,如圖1所示.
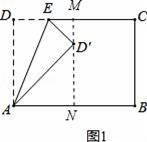

設DE=a,則D′E=a.
∵矩形ABCD有兩條對稱軸,
∴分兩種情況考慮:
①當DM=CM時,
AN=DM=
 CD=
CD=
 AB=4,AD=AD′=5,
AB=4,AD=AD′=5,
由勾股定理可知:
ND′=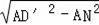
 =3,
=3,
∴MD′=MN﹣ND′=AD﹣ND′=2,EM=DM﹣DE=4﹣a,
∵ED′2=EM2+MD′2,即a2=(4﹣a)2+4,
解得:a=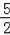
 ;
;
②當MD′=ND′時,
MD′=ND′=
 MN=
MN=
 AD=
AD=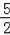
 ,
,
由勾股定理可知:
AN=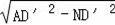
 =
=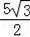
 ,
,
∴EM=DM﹣DE=AN﹣DE=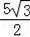
 ﹣a,
﹣a,
∵ED′2=EM2+MD′2,即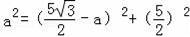
 ,
,
解得:a=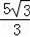
 .
.
綜上知:DE=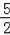
 或
或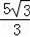
 .
.
故答案為:
 或
或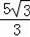
 .
.
【點評】本題考查了翻轉變換、軸對稱的性質、矩形的性質以及勾股定理,解題的關鍵是找出關于DM長度的一元二次方程.本題屬于中檔題,難度不大,但在做題過程中容易丟失一種情況,解決該題型題目時,結合勾股定理列出方程是關鍵.


 期末1卷素質教育評估卷系列答案
期末1卷素質教育評估卷系列答案科目:初中數學 來源: 題型:
如圖,把一塊含有45°角的直角三角板的兩個頂點放在直尺的對邊上.如果∠1=20°,那么∠2的度數是( )
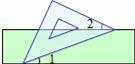

A.30° B.25° C.20° D.15°
查看答案和解析>>
科目:初中數學 來源: 題型:
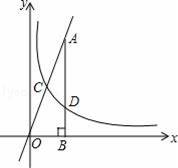
如圖,反比例函數y=
 (k≠0,x>0)的圖象與直線y=4x相交于點C,過直線上點A(2,8)作AB垂直于x軸于點B,交反比例函數圖象于點D,且AD=3BD.
(k≠0,x>0)的圖象與直線y=4x相交于點C,過直線上點A(2,8)作AB垂直于x軸于點B,交反比例函數圖象于點D,且AD=3BD.
(1)求k的值;
(2)求點C的坐標;
(3)在y軸上是否存在一點P,使點P到C、D兩點距離之和PC+PD最小?若存在,求出點P的坐標;若不存在,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com