
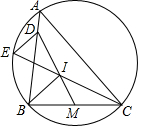
 M是BC邊的中點,I為內心,連接M、I交AB邊于D,連接CI交外接圓于E,證明:$\frac{DE}{EI}$=$\frac{BI}{CI}$.
M是BC邊的中點,I為內心,連接M、I交AB邊于D,連接CI交外接圓于E,證明:$\frac{DE}{EI}$=$\frac{BI}{CI}$. 分析 延長IM到F,使得MF=IM,延長CE交∠ABC的外角平分線于G,設CE交AB于N,∠B=2β,∠C=2α,連接CF、BF、GD、BE.首先證明DG∥BC,推出∠CGD=∠BCG=α,推出∠BGD=∠EBG+α=∠EGB+α=∠GBD,由△GDE≌△BDE,推出∠GDE=∠BDE,由DG∥BC,推出∠GDN=∠CBD=2β,推出∠BDE=β=∠DBI,推出DE∥BI∥CF,即可解決問題.
解答 證明:延長IM到F,使得MF=IM,延長CE交∠ABC的外角平分線于G,設CE交AB于N,∠B=2β,∠C=2α,連接CF、BF、GD、BE.
∵BM=CM,MF=IM,
∴四邊形IBFC是平行四邊形,
∴BI=CF,BF=CI,BF∥CI,
∵I是△ABC的內心,
∴∠ACE=∠BCE=α,∠ABI=∠CBI=β,∠ABE=∠BCE=α,
∵I是△ABC內心,G是△ABC的旁心,
∴∠GBI=90°,
∵∠EIB=α+β,∠EBI=α+β,
∴∠EBI=∠EIB,
∴EB=EI,
∵∠BGE+∠GIB=90°,∠EBG+∠EBI=90°,
∴∠EGB=∠EBG,
∴EG=EB=EI,
∵IN∥BF,
∴$\frac{DB}{DN}$=$\frac{BF}{NI}$=$\frac{CI}{NI}$①,
在△BCN中,由內外角平分線定理可知:$\frac{BC}{BN}$=$\frac{CL}{NI}$=$\frac{CG}{GN}$②,
由①②得到$\frac{DB}{DN}$=$\frac{CG}{GN}$,
∴$\frac{DB-DN}{DN}$=$\frac{CG-GN}{GN}$,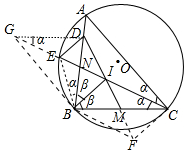
∴$\frac{BN}{DN}$=$\frac{CN}{GN}$,
∴DG∥BC,
∴∠CGD=∠BCG=α,
∴∠BGD=∠EBG+α=∠EGB+α=∠GBD,
∵DB=DG,DE=DE,EG=BE,
∴△GDE≌△BDE,
∴∠GDE=∠BDE,
∵DG∥BC,
∴∠GDN=∠CBD=2β,
∴∠BDE=β=∠DBI,
∴DE∥BI∥CF,
∴$\frac{DE}{EI}$=$\frac{CF}{CI}$=$\frac{BI}{CI}$.
點評 本題考查三角形內心、外心、全等三角形的判定和性質、平行四邊形的判定和性質,平行線的性質、角平分線的性質定理等知識,解題的關鍵是學會添加常用輔助線,題目比較難,屬于競賽題目.


科目:初中數學 來源: 題型:填空題
 如圖,在△ABC和△DCB中,AB=DC,AC與BD相交于點E,若不再添加任何字母與輔助線,要使△ABC≌△DCB,則還需增加的一個條件AC=BD.
如圖,在△ABC和△DCB中,AB=DC,AC與BD相交于點E,若不再添加任何字母與輔助線,要使△ABC≌△DCB,則還需增加的一個條件AC=BD.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
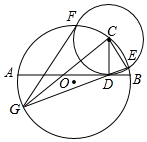 如圖,AB是⊙O的直徑,點C在⊙O上,⊙C與AB相切于點D,交⊙O于E、F兩點,連接ED并延長交⊙O于G點,連接CG、FG.
如圖,AB是⊙O的直徑,點C在⊙O上,⊙C與AB相切于點D,交⊙O于E、F兩點,連接ED并延長交⊙O于G點,連接CG、FG.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
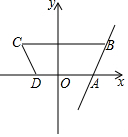 如圖,已知等腰梯形ABCD的面積為4k,點A的坐標是(x1,0),點B的坐標是(x2,1),點A、B在直線y=$\frac{1}{k}$x-1(k>0,k是不為0的常數)上,經過A、B、C、D四點的拋物線y=ax2+bx+c,它的頂點在直線y=(n-3)x+3-n上,
如圖,已知等腰梯形ABCD的面積為4k,點A的坐標是(x1,0),點B的坐標是(x2,1),點A、B在直線y=$\frac{1}{k}$x-1(k>0,k是不為0的常數)上,經過A、B、C、D四點的拋物線y=ax2+bx+c,它的頂點在直線y=(n-3)x+3-n上,查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖是某月的日歷表,在此日歷表上可以用一個矩形圈出3×3個位置的9個數(如6,7,8,13,14,15,20,21,22),若圈出的9個數中,最大數與最小數的和為46,則這9個數的和為207.
如圖是某月的日歷表,在此日歷表上可以用一個矩形圈出3×3個位置的9個數(如6,7,8,13,14,15,20,21,22),若圈出的9個數中,最大數與最小數的和為46,則這9個數的和為207.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
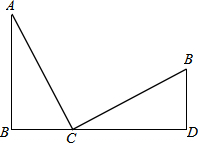 如圖,B、C、D三點在同一直線上,∠ABC=∠CDE=90°,且AC⊥EC,BC=DE.
如圖,B、C、D三點在同一直線上,∠ABC=∠CDE=90°,且AC⊥EC,BC=DE.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com