
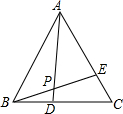
 如圖,已知等邊△ABC中,DC=EA,AD與BE相交于點P,求∠APB的度數.
如圖,已知等邊△ABC中,DC=EA,AD與BE相交于點P,求∠APB的度數. 分析 易證△BEA≌△ADC,即可求得∠ABE=∠CAD,根據三角形內角和為180°即可解題.
解答 解:∵△ABC是等邊三角形,
∴AB=AC,∠BAE=∠ACD=60°,
在△BEA和△ADC中,$\left\{\begin{array}{l}{DC=BA}&{\;}\\{∠BAE=∠ACD}&{\;}\\{AB=AC}&{\;}\end{array}\right.$
∴△BEA≌△ADC,(SAS)
∴∠ABE=∠CAD,
∵∠APB=180°-∠BAD-∠ABP,
∴∠APB=180°-∠CBP-∠ABP=180°-∠BAC=120°.
點評 本題考查了等邊三角形的性質、全等三角形的判定和性質;證明三角形全等是解決問題的關鍵.


科目:初中數學 來源: 題型:選擇題
| A. | 等腰三角形 | B. | 等邊三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
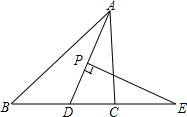 如圖,在△ABC中,AD平分∠BAC,P為線段AD上的一個點,PE⊥AD交直線BC于點E
如圖,在△ABC中,AD平分∠BAC,P為線段AD上的一個點,PE⊥AD交直線BC于點E查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,火焰的光線穿過小孔O,在豎直的屏幕上形成倒立的實像,像的長度BD=2cm,OA=60cm,OB=15cm,則火焰AC的長度為8cm.
如圖,火焰的光線穿過小孔O,在豎直的屏幕上形成倒立的實像,像的長度BD=2cm,OA=60cm,OB=15cm,則火焰AC的長度為8cm.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
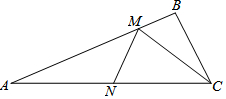 如圖:△ABC中,AC=$\sqrt{6}$,∠BAC=22.5°,點M、N分別是射線AB和AC上動點,則CM+MN的最小值是( )
如圖:△ABC中,AC=$\sqrt{6}$,∠BAC=22.5°,點M、N分別是射線AB和AC上動點,則CM+MN的最小值是( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{6}$ | D. | 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com