
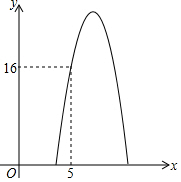
 某商品的進價為每個3元,已知該商品每天的銷售利潤y(元)與銷售單價x(元)之間滿足關系y=ax2+16x+c,其圖象如圖所示.
某商品的進價為每個3元,已知該商品每天的銷售利潤y(元)與銷售單價x(元)之間滿足關系y=ax2+16x+c,其圖象如圖所示.分析 (1)利用待定系數法求二次函數解析式得出即可;
(2)利用配方法求出二次函數最值即可;
(3)根據題意令y=16,解方程可得x的值,結合圖象可知x的范圍.
解答 解:(1)y=ax2+16x+c圖象過點(3,0)、(5,16),
∴$\left\{\begin{array}{l}{9a+48+c=0}\\{25a+80+c=16}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{c=-39}\end{array}\right.$.
(2)∵y=-x2+16x-39=-(x-8)2+25,
∴當x=8時,y最大=25.
答:銷售單價為8元時,該種商品每天的銷售利潤最大,最大利潤為25元;
(3)根據題意,當y=16時,得:-x2+16x-39=16,
解得:x1=5,x2=11,
即銷售單價5≤x≤11時,該種商品每天的銷售利潤不低于16元.
點評 本題考查了二次函數的應用以及待定系數法求二次函數解析式等知識,正確利用二次函數圖象是解題關鍵.


科目:初中數學 來源: 題型:選擇題
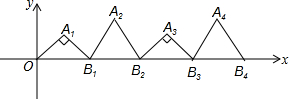 如圖,在平面直角坐標系的第一象限內,依次作等腰直角三角形OA1B1,正三角形B1A2B2,等腰直角三角形B2A3B3,…,且∠A1=∠A3=∠A5=…=90°,B1坐標為(2,0),B2坐標為(4,0),B3坐標為(6,0),…,按這樣的規律,點A2015的坐標是( )
如圖,在平面直角坐標系的第一象限內,依次作等腰直角三角形OA1B1,正三角形B1A2B2,等腰直角三角形B2A3B3,…,且∠A1=∠A3=∠A5=…=90°,B1坐標為(2,0),B2坐標為(4,0),B3坐標為(6,0),…,按這樣的規律,點A2015的坐標是( )| A. | (4029,1) | B. | (2015,$\sqrt{3}$) | C. | (4030,1) | D. | (4029,$\sqrt{3}$) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
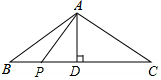 如圖,等腰△ABC的底邊BC=8cm,腰AC=5cm,AD是底邊BC上的高,一動點P在底邊上從點B開始向點C以0.25cm/s的速度移動,設運動時間為t(s).
如圖,等腰△ABC的底邊BC=8cm,腰AC=5cm,AD是底邊BC上的高,一動點P在底邊上從點B開始向點C以0.25cm/s的速度移動,設運動時間為t(s).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com