
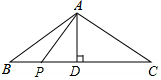
 如圖,等腰△ABC的底邊BC=8cm,腰AC=5cm,AD是底邊BC上的高,一動(dòng)點(diǎn)P在底邊上從點(diǎn)B開始向點(diǎn)C以0.25cm/s的速度移動(dòng),設(shè)運(yùn)動(dòng)時(shí)間為t(s).
如圖,等腰△ABC的底邊BC=8cm,腰AC=5cm,AD是底邊BC上的高,一動(dòng)點(diǎn)P在底邊上從點(diǎn)B開始向點(diǎn)C以0.25cm/s的速度移動(dòng),設(shè)運(yùn)動(dòng)時(shí)間為t(s).分析 (1)根據(jù)等腰三角形三線合一性質(zhì)可得到BD的長(zhǎng),由勾股定理可求得AD的長(zhǎng);
(2)先求出P點(diǎn)移動(dòng)的路程BP,再除以速度即可;
(3)分兩種情況進(jìn)行分析:①PA⊥AC②PA⊥BC,從而可得到運(yùn)動(dòng)的時(shí)間.
解答  解:(1)∵等腰△ABC的底邊BC=8cm,AD是底邊BC上的高,
解:(1)∵等腰△ABC的底邊BC=8cm,AD是底邊BC上的高,
∴BD=CD=$\frac{1}{2}$BC=4cm,
∵腰AC=5cm,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=3cm;
(2)∵PC=AC=5cm,
∴BP=BC-PC=3cm,
∵動(dòng)點(diǎn)P在底邊上從點(diǎn)B開始向點(diǎn)C以0.25cm/s的速度移動(dòng),
∴t=3÷0.25=12s.
故答案為12;
(3)分兩種情況:
①當(dāng)點(diǎn)P運(yùn)動(dòng)t秒后有PA⊥AC時(shí),
∵AP2=PD2+AD2=PC2-AC2,
∴PD2+AD2=PC2-AC2,
∴PD2+32=(PD+4)2-52,
∴PD=2.25,
∴BP=4-2.25=1.75=0.25t,
∴t=7秒;
當(dāng)點(diǎn)P運(yùn)動(dòng)t秒后有PA⊥BC時(shí),即P與D重合,
∵BP=BD=4=0.25t,
∴t=16秒,
∴點(diǎn)P運(yùn)動(dòng)的時(shí)間為7秒或16秒.
點(diǎn)評(píng) 本題考查了等腰三角形的性質(zhì),勾股定理,利用數(shù)形結(jié)合以及分類討論是解題的關(guān)鍵.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | (5,-8) | B. | (-5,-8) | C. | (5,8) | D. | (8,-5) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
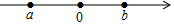 實(shí)數(shù)a,b,在數(shù)軸上大致位置如圖,則a,b,的大小關(guān)系是( )
實(shí)數(shù)a,b,在數(shù)軸上大致位置如圖,則a,b,的大小關(guān)系是( )| A. | a<0<b | B. | b<a<0 | C. | 0<b<a | D. | a>0>b |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
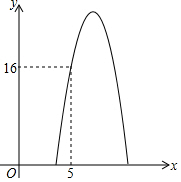 某商品的進(jìn)價(jià)為每個(gè)3元,已知該商品每天的銷售利潤(rùn)y(元)與銷售單價(jià)x(元)之間滿足關(guān)系y=ax2+16x+c,其圖象如圖所示.
某商品的進(jìn)價(jià)為每個(gè)3元,已知該商品每天的銷售利潤(rùn)y(元)與銷售單價(jià)x(元)之間滿足關(guān)系y=ax2+16x+c,其圖象如圖所示.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | $\overrightarrow{a}$∥$\overrightarrow{b}$,$\overrightarrow{c}$∥$\overrightarrow{b}$ | B. | $\overrightarrow{a}$+3$\overrightarrow{c}$=$\overrightarrow{0}$,$\overrightarrow{b}$=3$\overrightarrow{c}$ | C. | $\overrightarrow{a}$=-3$\overrightarrow{b}$ | D. | |$\overrightarrow{a}$|=3|$\overrightarrow{b}$| |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com