
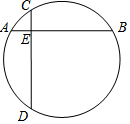
 如圖,AB,CD是⊙O的弦,AB⊥CD,且AE=$\sqrt{3}$,EB=3$\sqrt{3}$,$\widehat{AB}$的度數(shù)為120°.解答問題:
如圖,AB,CD是⊙O的弦,AB⊥CD,且AE=$\sqrt{3}$,EB=3$\sqrt{3}$,$\widehat{AB}$的度數(shù)為120°.解答問題:分析 (1)分別作AB和CD的垂直平分線,它們的交點(diǎn)為點(diǎn)O;
(2)連接OB,AB的垂直平分線交AB于F,如圖,根據(jù)垂徑定理得到AF=BF,利用圓心角、弧、弦的關(guān)系得到∠BOF=60°,然后在Rt△BOF中利用∠BOF的正弦可求出OB;
(3)CD的垂直平分線交CD于H,連接OD,如圖,易得四邊形OFEH為矩形,則OH=EF=$\sqrt{3}$,則在Rt△OHD中利用勾股定理可計(jì)算出DH=$\sqrt{13}$,然后根據(jù)垂徑定理得到CD=2DH=2$\sqrt{13}$.
解答 解:(1)如圖,點(diǎn)O為所作;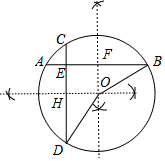
(2)連接OB,AB的垂直平分線交AB于F,如圖,
∵OF⊥AB,
∴AF=BF,∠BOF=$\frac{1}{2}$×120°=60°,
∵AE=$\sqrt{3}$,EB=3$\sqrt{3}$,$\widehat{AB}$
∴AF=BF=2$\sqrt{3}$,
在Rt△BOF中,∵sin∠BOF=$\frac{BF}{OB}$,
∴OB=$\frac{2\sqrt{3}}{sin60°}$=4,
即⊙O的半徑為4;
(3)CD的垂直平分線交CD于H,連接OD,如圖,
∵AF=2$\sqrt{3}$,AF=$\sqrt{3}$,
∴EF=$\sqrt{3}$,
易得四邊形OFEH為矩形,
∴OH=EF=$\sqrt{3}$,
在Rt△OHD中,DH=$\sqrt{O{D}^{2}-O{H}^{2}}$=$\sqrt{{4}^{2}-(\sqrt{3})^{2}}$=$\sqrt{13}$,
∵OH⊥CD,
∴CH=DH,
∴CD=2DH=2$\sqrt{13}$.
點(diǎn)評(píng) 本題考查了作圖-復(fù)雜作圖:復(fù)雜作圖是在五種基本作圖的基礎(chǔ)上進(jìn)行作圖,一般是結(jié)合了幾何圖形的性質(zhì)和基本作圖方法.解決此類題目的關(guān)鍵是熟悉基本幾何圖形的性質(zhì),結(jié)合幾何圖形的基本性質(zhì)把復(fù)雜作圖拆解成基本作圖,逐步操作.也考查了垂徑定理和解直角三角形.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 15 | B. | 30 | C. | $\sqrt{30}$ | D. | 15π |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
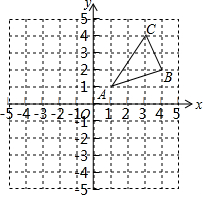 如圖,△ABC三個(gè)頂點(diǎn)的坐標(biāo)分別為A(1,1),B(4,2),C(3,4).
如圖,△ABC三個(gè)頂點(diǎn)的坐標(biāo)分別為A(1,1),B(4,2),C(3,4).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 任意買一張電影票,座位號(hào)是偶數(shù) | B. | 367人中至少有2人的生日相同 | ||
| C. | 擲一次骰子,向上的一面是6點(diǎn) | D. | 某射擊運(yùn)動(dòng)員射擊1次,命中靶心 |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com