
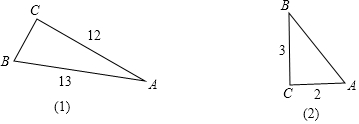
分析 根據(jù)勾股定理,可得直角三角形的另一邊,根據(jù)正弦函數(shù)是對邊比斜邊,余弦函數(shù)是鄰邊比斜邊,正切函數(shù)是對邊比鄰邊,可得答案.
解答 解:(1)由勾股定理,得
BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=5,
sinA=$\frac{BC}{AB}$=$\frac{5}{13}$,cosA=$\frac{AC}{AB}$=$\frac{12}{13}$,tanA=$\frac{BC}{AC}$=$\frac{5}{12}$,
sinB=$\frac{AC}{AB}$=$\frac{12}{13}$,cosB=$\frac{BC}{AB}$=$\frac{5}{13}$,tanB=$\frac{AC}{BC}$=$\frac{12}{5}$;
(2)由勾股定理,得
AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{13}$,
sinA=$\frac{BC}{AB}$=$\frac{3\sqrt{13}}{13}$,cosA=$\frac{AC}{AB}$=$\frac{2\sqrt{13}}{13}$,tanA=$\frac{BC}{AB}$=$\frac{3}{2}$,
sinB=$\frac{AC}{AB}$=$\frac{2\sqrt{13}}{13}$,cosB=$\frac{BC}{AB}$=$\frac{3\sqrt{13}}{13}$,tanB=$\frac{AC}{BC}$=$\frac{2}{3}$.
點(diǎn)評 本題考查了銳角三角函數(shù),利用銳角三角函數(shù)的定義是解題關(guān)鍵.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
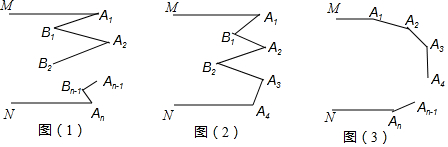
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
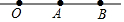 如圖,O,A,B三點(diǎn)在同一直線上,則下列說法中正確的是( )
如圖,O,A,B三點(diǎn)在同一直線上,則下列說法中正確的是( )| A. | 射線OA與射線AO表示同一條射線 | B. | 射線OA大于射線AB | ||
| C. | 射線OA與射線OB表示同一條射線 | D. | 線段OA與線段AO表示兩條不同線段 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
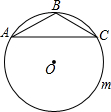 如圖,△ABC中,AB=BC,∠ABC=120°,AC=2$\sqrt{3}$,⊙O是△ABC的外接圓,D是優(yōu)弧AmC上任意一點(diǎn)(不包括A,C),記四邊形ABCD的周長為y,BD的長為x,則y關(guān)于x的函數(shù)關(guān)系式是( )
如圖,△ABC中,AB=BC,∠ABC=120°,AC=2$\sqrt{3}$,⊙O是△ABC的外接圓,D是優(yōu)弧AmC上任意一點(diǎn)(不包括A,C),記四邊形ABCD的周長為y,BD的長為x,則y關(guān)于x的函數(shù)關(guān)系式是( )| A. | y=$\frac{\sqrt{3}}{4}$x+4 | B. | y=$\sqrt{3}$x+4 | C. | y=$\sqrt{3}$x2+4 | D. | y=$\frac{\sqrt{3}}{4}$x2+4 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com