
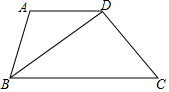
 如圖,在梯形ABCD中,AD∥BC,BD平分∠ABC,且CD⊥BD,若AD=5,BD=CD+2,則tan∠DBC=$\frac{3}{4}$.
如圖,在梯形ABCD中,AD∥BC,BD平分∠ABC,且CD⊥BD,若AD=5,BD=CD+2,則tan∠DBC=$\frac{3}{4}$. 分析 設CD=x,則BD=x+2,證出AB=AD=5,得出BE=$\frac{1}{2}$BD=$\frac{1}{2}$x+1,證明△ABE∽△CBD,得出比例式求出BC=10,由勾股定理求出CD,得出BD,再由三角函數定義即可得出結果.
解答 解:作AE⊥BD于E,如圖所示: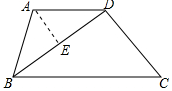
則∠AEB=90°,
設CD=x,則BD=x+2,
∵AD∥BC,
∴∠ADB=∠CBD,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD=5,
∴BE=$\frac{1}{2}$BD=$\frac{1}{2}$x+1,
∵CD⊥BD,
∴∠BDC=90°=∠BEA,
又∵∠ABD=∠CBD,
∴△ABE∽△CBD,
∴$\frac{BE}{AB}=\frac{BD}{BC}$,即$\frac{\frac{1}{2}x+1}{5}=\frac{x+2}{bc}$,
解得:BC=10,
在Rt△BCD中,CD2+BD2=BC2,
即x2+(x+2)2=102,
解得:x=6,
∴CD=6,BD=8,
∴tan∠DBC=$\frac{6}{8}$=$\frac{3}{4}$
故答案為:$\frac{3}{4}$.
點評 本題考查了梯形的性質、等腰三角形的判定、相似三角形的判定與性質、勾股定理以及三角函數;證明三角形相似求出BC是解決問題的關鍵.


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:初中數學 來源: 題型:選擇題
| A. | 2017 | B. | 1 | C. | 2016 | D. | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{20}$是無理數 | B. | 4<$\sqrt{20}$<5 | ||
| C. | $\sqrt{20}$是20的算術平方根 | D. | $\sqrt{20}$不能再化簡 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
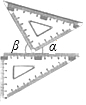 數學課上,小麗把一副三角板按如圖所示的位置擺放(其中一個三角板的直角頂點在另一個三角板的直角邊上),如果∠α=28°,那么∠β=62°.
數學課上,小麗把一副三角板按如圖所示的位置擺放(其中一個三角板的直角頂點在另一個三角板的直角邊上),如果∠α=28°,那么∠β=62°.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com