
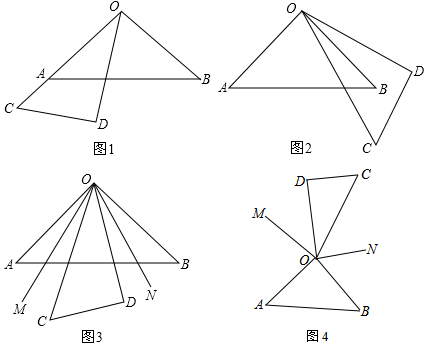
分析 (1)由圖可得角之間的關系:∠BOD=90°-∠COD,∠AOC=90°-$\frac{1}{2}$∠COD,據此解答;
(2))由圖可得角之間的關系:∠MON=$\frac{1}{2}$(∠AOB-∠COD)+∠COD,于是得到結論;
(3)由圖可得角之間的關系;∠MON=∠MOC+∠NOD-30°,于是得到結論.
解答 解:∵∠BAC+∠ABP+∠BPF+∠AFP=360°,且∠BPF+∠BAC=180°,
∴∠ABP+∠AFP=180°,
(1)∵OB平分∠COD,∠COD=30°,
∴∠BOC=$\frac{1}{2}$∠COD=15°,
∴∠AOC=∠AOB-∠BOC=90°-15°=75°,
(2)∵∠AOB=90°,∠COD=30°,
∴∠AOC+∠BOD=90°-30°=60°,
∵OM平分∠AOC,ON平分∠BOD,
∴∠MOC+∠NOD=$\frac{1}{2}$∠AOC+∠BOD)=30°,
∴∠MON=∠COD+∠MOC+∠NOD=30°+30°=60°,
(3)∵∠AOB=90°,∠COD=30°,
∴∠AOC+∠BOD=360°-90°+∠COD=300°,
∵OM平分∠AOC,ON平分∠BOD,
∴∠MOC+∠NOD=$\frac{1}{2}$(∠AOC+∠BOD)=150°,
∴∠MON=∠MOC+∠NOD-∠COD=150°-30°=120°.
點評 本題考查了角的計算,難點是找出變化過程中的不變量,需要結合圖形來計算,對同學們的作圖、分析、計算能力有較高要求.在計算分析的過程中注意動手操作,在旋轉的過程中得到不變的量.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖所示,一次函數y=-$\frac{2}{3}$x+2的圖象分別與x軸、y軸交于點A、B,以線段AB為邊在第一象限內作等腰直角△ABC,∠BAC=90°,試求經過B、C兩點的直線的函數表達式.
如圖所示,一次函數y=-$\frac{2}{3}$x+2的圖象分別與x軸、y軸交于點A、B,以線段AB為邊在第一象限內作等腰直角△ABC,∠BAC=90°,試求經過B、C兩點的直線的函數表達式.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
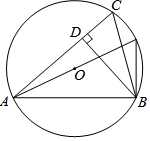 如圖,已知⊙O的半徑為5,銳角△ABC內接于⊙O,BD⊥AC于點D,AB=8,則sin∠CBD的值等于( )
如圖,已知⊙O的半徑為5,銳角△ABC內接于⊙O,BD⊥AC于點D,AB=8,則sin∠CBD的值等于( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
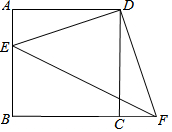 如圖,四邊形ABCD是正方形,E、F分別是AB和BC延長線上的點,且AE=CF.
如圖,四邊形ABCD是正方形,E、F分別是AB和BC延長線上的點,且AE=CF.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 小明和小強分別從A、B兩地出發勻速相向而行,達到對方出發地后均立即以原速返回.已知小明到達B地半小時后,小強到達A地.如圖表示他們出發時間t(單位:小時)與距離A地的路程S(單位:千米)之間的關系圖,則出發后$\frac{45}{11}$小時,小明和小強第2次相遇.
小明和小強分別從A、B兩地出發勻速相向而行,達到對方出發地后均立即以原速返回.已知小明到達B地半小時后,小強到達A地.如圖表示他們出發時間t(單位:小時)與距離A地的路程S(單位:千米)之間的關系圖,則出發后$\frac{45}{11}$小時,小明和小強第2次相遇.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com