
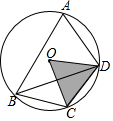
分析 (1)根據(jù)題意可得$\widehat{BD}$=2$\widehat{CD}$,進而可得∠BAD=∠COD,∠BAD=2∠CBD,再由條件∠CBD=30°可得∠BAD的度數(shù);
(2)根據(jù)圓周角定理可得∠COD=60°,再根據(jù)扇形的面積公式可得答案.
解答 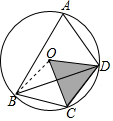 解:(1)∵C是為$\widehat{DB}$的中點,
解:(1)∵C是為$\widehat{DB}$的中點,
∴$\widehat{BD}$=2$\widehat{CD}$,
∴∠BAD=∠COD,
∵$\widehat{CD}$=$\widehat{CD}$,
∴∠COD=2∠CBD,
∴∠BAD=2∠CBD,
∵∠CBD=30°,
∴∠BAD=60°;
(2)∵$\widehat{CD}$=$\widehat{CD}$,
∴∠COD=2∠CBD,
∵∠CBD=30°,
∴∠COD=60°,
則S扇形OCD=$\frac{60×1{2}^{2}π}{360}$=24π.
點評 此題主要考查了圓周角定理,以及扇形的面積計算,關(guān)鍵是掌握在同圓或等圓中,同弧或等弧所對的圓周角相等,都等于這條弧所對的圓心角的一半.


科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
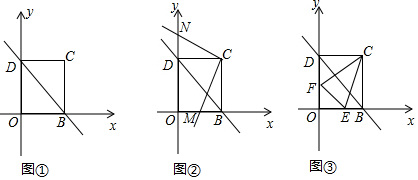
 如圖所示,二次函數(shù)y=ax2+bx+c(a≠0)的圖象,有下列4個結(jié)論:①abc>0;②b>a+c;③4a+2b+c>0;④b2-4ac>0;其中正確的是③④.
如圖所示,二次函數(shù)y=ax2+bx+c(a≠0)的圖象,有下列4個結(jié)論:①abc>0;②b>a+c;③4a+2b+c>0;④b2-4ac>0;其中正確的是③④.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 1道 | B. | 2道 | C. | 3道 | D. | 4道 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | ±1 | B. | 1 | C. | -1 | D. | 0 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com