
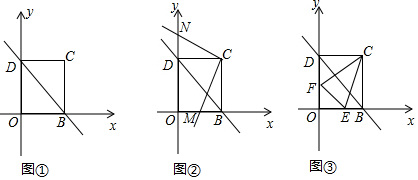
分析 (1)根據折疊的性質證明矩形OBCD是正方形,得到答案;
(2)證明△DCN≌△BCM,根據全等三角形的性質解答;
(3)以點C為旋轉中心把△CDF逆時針旋轉90°,得到△CBH,證明△FCE≌△HCE,求出△OEF的周長是定值.
解答 解:(1)∵OB=OD,
∴∠ODB=∠OBD=45°,
由折疊的性質可知,∠OBC=2∠OBD=90°,∠ODC=2∠ODB=90°,
又∠DOB=90°,
∴四邊形OBCD是矩形,又OB=OD,
∴矩形OBCD是正方形,
∴點C的坐標為(3,3)
故答案為3;3;
(2)∵∠MCN=90°,∠DCB=90°,
∴∠DCN=∠BCM,
在△DCN和△BCM中,
$\left\{\begin{array}{l}{∠DCM=∠BCN}\\{CD=CB}\\{∠CDN=∠CBM}\end{array}\right.$,
∴△DCN≌△BCM,
∴DN=BM,
∴m+n=OB-BN+OD+DN=OB+OD=6;
(3)△OEF的周長是定值6,
以點C為旋轉中心把△CDF逆時針旋轉90°,得到△CBH,
∵∠ECF=45°,∠DCB=90°,
∴∠DCF+∠ECB=45°,
∴∠ECH=45°,
在△FCE和△HCE中,
$\left\{\begin{array}{l}{∠CF=CH}\\{∠FCE=∠HCE}\\{CE=CE}\end{array}\right.$,
∴△FCE≌△HCE,
∴EF=EH,
∴△OEF的周長=OF+OE+EF=OF+OE+BE+DF=3+3=6.
點評 本題考查的是全等三角形的判定和性質、軸對稱的性質,掌握全等三角形的判定定理和性質定理是解題的關鍵.


 中考利劍中考試卷匯編系列答案
中考利劍中考試卷匯編系列答案科目:初中數學 來源: 題型:解答題
 在如圖所示的正方形網格中,每個小正方形的邊長均為1,格點三角形ABC(頂點是網格線交點的三角形)的頂點A、C的坐標分別為(-4,5)、(-1,3)
在如圖所示的正方形網格中,每個小正方形的邊長均為1,格點三角形ABC(頂點是網格線交點的三角形)的頂點A、C的坐標分別為(-4,5)、(-1,3)查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 五個完全相同的小長方形拼成如圖所示的大長方形,大長方形的周長是32cm,則小長方形的面積是( )
五個完全相同的小長方形拼成如圖所示的大長方形,大長方形的周長是32cm,則小長方形的面積是( )| A. | 8cm2 | B. | 10cm2 | C. | 12cm2 | D. | 16cm2 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (2,3) | B. | (-2,3) | C. | (-3,2) | D. | (-3,-2) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
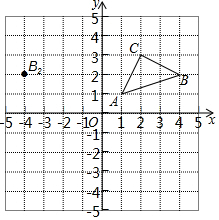 如圖所示,在直角坐標系xOy中,△ABC三點的坐標分別為A(1,1),B(4,2),C(2,3).
如圖所示,在直角坐標系xOy中,△ABC三點的坐標分別為A(1,1),B(4,2),C(2,3).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com