
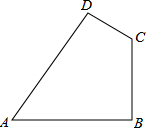
 如圖,已知四邊形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A與∠C關系是互補.
如圖,已知四邊形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A與∠C關系是互補. 分析 連接AC,然后根據勾股定理求出AC的值,然后根據勾股定理的逆定理判斷△ADC為Rt△,然后根據四邊形的內角和定理即可得到∠A與∠C關系.
解答 解:∠A與∠C關系為:互補.理由如下:
連結AC,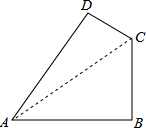
∵∠ABC=90°,
∴在Rt△ABC中,由勾股定理得:
AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=25cm,
∵AD2+DC2=625=252=AC2,
∴△ADC是直角三角形,且∠D=90°,
∵∠DAB+∠B+∠BCD+∠D=180°,
∴∠DAB+∠BCD=180°,
即∠A+∠C=180°,
故答案為:互補.
點評 此題考查了勾股定理及勾股定理的逆定理,解題的關鍵是:根據勾股定理的逆定理判斷△ADC是直角三角形.


 華東師大版一課一練系列答案
華東師大版一課一練系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中數學 來源: 題型:填空題
 有一塔形幾何體由若干個正方體構成,構成方式如圖所示,上層正方體下底面的四個頂點是下層正方體上底面各邊的中點.已知最底層正方體的棱長為2,且該塔形的表面積(含最底層正方體的底面面積)超過39,則該塔形中正方體的個數至少是6.
有一塔形幾何體由若干個正方體構成,構成方式如圖所示,上層正方體下底面的四個頂點是下層正方體上底面各邊的中點.已知最底層正方體的棱長為2,且該塔形的表面積(含最底層正方體的底面面積)超過39,則該塔形中正方體的個數至少是6.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,AB是⊙O的直徑,C,D在⊙O上,CD=AD,分別延長CD、BA相交于點E,且AE=$\sqrt{2}$OA,若BC=6,求⊙O的半徑.
如圖,AB是⊙O的直徑,C,D在⊙O上,CD=AD,分別延長CD、BA相交于點E,且AE=$\sqrt{2}$OA,若BC=6,求⊙O的半徑.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com