Question

14．如圖，C為線段BD上一動點，分別過點B、D作AB⊥BD，ED⊥BD，連接AC、EC，AB=5，DE=1，BD=8，設CD=x．
（1）直接寫出AC+CE的值；（用含x的代數式表示）
（2）求AC+CE的最小值．

Answer 1

分析 （1）根據線段的和差，可得BC的長，根據勾股定理，可得答案；
（2）根據兩點之間線段最短，可得線段AC+CE的最小值=AE，根據勾股定理，可得答案．

解答 解：（1）由線段的和差，得
BC=（8-x）．
由勾股定理，得
AC+CE=$\sqrt{A{B}^{2}+B{C}^{2}}$+$\sqrt{C{D}^{2}+D{E}^{2}}$=$\sqrt{{5}^{2}+（5-x）^{2}}$+$\sqrt{1+{x}^{2}}$=$\sqrt{（8-x）^{2}+25}$+$\sqrt{{x}^{2}+1}$；
（2）如圖，作CF⊥AB于F點．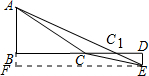
，
四邊形BDEF是矩形，
BF=DE=1，EF=BD=8，
AF=AB+BF=5+1=6，
AC+CE的最小值=AE=$\sqrt{A{F}^{2}+E{F}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10．

點評 本題考查了軸對稱-最短路線問題，（1）利用勾股定理；（2）利用兩點之間線段最短得出C₁的位置是解題關鍵．