国产婷婷色一区二区三区,中文字字幕在线,高清一区二区

精英家教網 > 初中數學 > 題目詳情

2．

如圖，直線y₁=kx+b過點A（0，3），且與直線y₂=mx交于點P（1，m），則不等式組mx＞kx+b＞mx-2的解集是（　　）

A．

x＞1

B．

1＜x＜$\frac{5}{3}$

C．

1＜x＜2

D．

1＜x＜3

分析先把A點代入y+kx+b得b=3，再把P（1，m）代入y=kx+3得k=m-3，接著解（m-3）x+3＞mx-2得x＜$\frac{5}{3}$，然后利用函數圖象可得不等式組mx＞kx+b＞mx-2的解集．

解答解：把P（1，m）代入y=kx+3得k+3=m，解得k=m-3，
解（m-3）x+3＞mx-2得x＜$\frac{5}{3}$，
所以不等式組mx＞kx+b＞mx-2的解集是1＜x＜$\frac{5}{3}$．
故選B．

點評本題考查了一次函數與一元一次不等式：從函數的角度看，就是尋求使一次函數y=kx+b的值大于（或小于）0的自變量x的取值范圍；從函數圖象的角度看，就是確定直線y=kx+b在x軸上（或下）方部分所有的點的橫坐標所構成的集合．

練習冊系列答案

豫欣圖書自主課堂系列答案

假期伙伴寒假大連理工大學出版社系列答案

藍博士暑假作業甘肅少年兒童出版社系列答案

快樂暑假新疆美術攝影出版社系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：初中數學 來源： 題型：選擇題

12．下列命題中，為真命題的是（　　）

	A．	對頂角相等		B．	同位角相等
	C．	若a²=b²，則a=b		D．	同旁內角相等，兩直線平行

查看答案和解析>>

科目：初中數學 來源： 題型：解答題

13．

如圖，直線AB，CD相交于點O，射線OE平分∠DOB，已知∠AOC=60°，求∠AOE的度數．

查看答案和解析>>

科目：初中數學 來源： 題型：選擇題

10．上課時，李老師在黑板上寫了一個實數，學生A，B，C，D爭先恐后地說出了這個數的一些特征：
學生A：在數軸上表示這個數的點在原點的左邊；
學生B：它是一個無理數；
學生C：它的絕對值小于2；
學生D：它的平方大于1．
老師表揚了A，B，C，D四個學生，因為他們都說對了，現在，請你猜猜看，老師在黑板上寫下的這個數可能是下列四個數中哪一個？（　　）

A．

$\sqrt{3}$

B．

-$\sqrt{2}$

C．

$-\sqrt{5}$

D．

-1.5

查看答案和解析>>

科目：初中數學 來源： 題型：解答題

17．計算：
（1）$\frac{1}{3}$+（-$\frac{3}{4}$）-（-$\frac{2}{3}$）
（2）（$\frac{7}{9}$$-\frac{5}{6}$$+\frac{3}{4}$）×（-36）
（3）$-\sqrt{\frac{4}{25}}$$-\root{3}{-\frac{8}{125}}$
（4）-3²+（-$\frac{1}{6}$）×（-6）-（-2）⁴÷8．

查看答案和解析>>

科目：初中數學 來源： 題型：解答題

7．

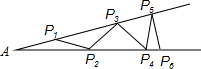課本“目標與評定”中有這樣一道思考題，如圖鋼架中，∠A=20°，焊上等長的鋼條來加固鋼架，若AP₁=P₁P₂，問這樣的鋼條至多需要多少根？
（1）請補充完整如下解答：
解：由題意可知，P₁P₂=P₂P₃=P₃P₄=P₄P₅=…
∵∠A=20°，AP₁=P₁P₂，
∴∠AP₂P₁=∠A．
∴∠P₂P₁P₃=∠P₁P₃P₂=40°，
同理可得，∠P₃P₂P₄=∠P₂P₄P₃=60°，
∠P₄P₃P₅=∠P₄P₅P₃=80°．
∴∠P₅P₄B=100°＞90°，
∴對于直線P₄B上任意一點P₆（點P₄除外），P₄P₅＜P₅P₆，
∴這樣的鋼條至多需要4根．
（2）繼續探究：當∠A=15°時，這樣的鋼條至多需要多少根？

查看答案和解析>>

科目：初中數學 來源： 題型：填空題

14．2016年，杭州緊抓服務保障G20峰會的有利機遇，經濟運行繼續保持了較好的發展勢頭，1-3季度實現地區生產總值（GDP）7780.67億元，按可比價格計算，同比增長10.0%，其中前一數據用科學記數法表示約為7.78067×10³億元．

查看答案和解析>>

科目：初中數學 來源： 題型：選擇題

11．-2017的相反數是（　　）

A．

-2017

B．

2017

C．

±2017