
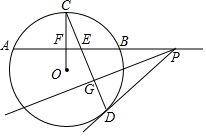
 如圖,在⊙O中,OC⊥AB于點F,弦CD交弦AB于點E,線段ED的垂直平分線GP交AB延長線于點P,連結PD.
如圖,在⊙O中,OC⊥AB于點F,弦CD交弦AB于點E,線段ED的垂直平分線GP交AB延長線于點P,連結PD.分析 (1)如圖,連接OD,欲證明PD是切線,只要證明∠ODP=90°即可.
(2)作OM⊥CD于M,則CM=DM=8,只要證明∠PDC=∠DOM,可得sin∠PDC=sin∠DOM=$\frac{DM}{OD}$,由此即可解決問題.
解答 (1)證明:如圖,連接OD,
∵PG垂直平分線段DE,
∴PE=PD,
∴∠PED=∠PDE,
∵OC⊥AB,
∴∠EFC=90°,
∴∠FCE+∠FEC=90°,
∵OC=OD,
∴∠OCD=∠ODC,
∵∠FEC=∠PED=∠PDF,
∴∠ODC+∠PDC=90°,
∴∠ODP=90°,
∴OD⊥PD,
∴PD是⊙O的切線.
(2)解:作OM⊥CD于M,則CM=DM=8,
∵∠PDC+∠ODC=90°,○ODC+∠DOM=90°,
∴∠PDC=∠DOM,
∴sin∠PDC=sin∠DOM=$\frac{DM}{OD}$=$\frac{8}{10}$=$\frac{4}{5}$.
點評 本題考查切線的判定和性質、線段的垂直平分線的性質、圓周角定理、銳角三角函數等知識,解題的關鍵是靈活運用所學知識解決問題,屬于中考常考題型.


 名校通行證有效作業系列答案
名校通行證有效作業系列答案科目:初中數學 來源: 題型:解答題
 如圖,已知AB=AC,AD=AE,∠1=∠2,試說明BD=CE的理由.
如圖,已知AB=AC,AD=AE,∠1=∠2,試說明BD=CE的理由.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在△ABC中,∠ACB=90°,AC=BC,D為AB的中點.將△ACD繞點C逆時針旋轉90°到△BCE.
如圖,在△ABC中,∠ACB=90°,AC=BC,D為AB的中點.將△ACD繞點C逆時針旋轉90°到△BCE.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,平面直角坐標系中,拋物線y=-$\frac{3}{4}$x2+$\frac{9}{4}$x+3交x軸交于點A、B,交y軸于點C,點P從O出發,以每秒1個單位的速度向終點B運動,同時點Q從B出發,以每秒1個單位的速度向終點O運動,過點Q作DQ⊥x軸,交BC于點D,連接CP、DP.設運動時間為t.
如圖,平面直角坐標系中,拋物線y=-$\frac{3}{4}$x2+$\frac{9}{4}$x+3交x軸交于點A、B,交y軸于點C,點P從O出發,以每秒1個單位的速度向終點B運動,同時點Q從B出發,以每秒1個單位的速度向終點O運動,過點Q作DQ⊥x軸,交BC于點D,連接CP、DP.設運動時間為t.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
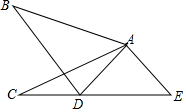 如圖,在△ABD和△ACE中,有下列論斷:①AB=AC;②AD=AE;③∠B=∠C;④BD=CE.請以其中三個論斷作為條件,另一個論斷作為結論,寫出一個真命題:如果AB=AC,AD=AE,BD=CE,那么∠B=∠C.
如圖,在△ABD和△ACE中,有下列論斷:①AB=AC;②AD=AE;③∠B=∠C;④BD=CE.請以其中三個論斷作為條件,另一個論斷作為結論,寫出一個真命題:如果AB=AC,AD=AE,BD=CE,那么∠B=∠C.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com