Question

4．為給人們的生活帶來方便，2017年興化市準備在部分城區實施公共自行車免費服務．圖1是公共自行車的實物圖，圖2是公共自行車的車架示意圖，點A、D、C、E在同一條直線上，CD=35cm，DF=24cm，AF=30cm，FD⊥AE于點D，座桿CE=15cm，且∠EAB=75°．
（1）求AD的長；
（2）求點E到AB的距離（結果保留整數）．
（參考數據：sin75°≈0.97，cos75°≈0.26，tan75°≈3.73）

Answer 1

分析 （1）利用勾股定理可求得AD的長；
（2）過點E作EH⊥AB，垂足為H，利用∠EAH的正弦列式求EH的長即可．

解答 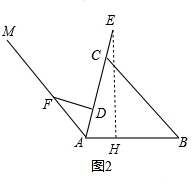解：（1）在Rt△ADF中，AF=30，DF=24，
由勾股定理得：AD=$\sqrt{A{F}^{2}-D{F}^{2}}$=$\sqrt{3{0}^{2}-2{4}^{2}}$=18cm；
（2）過點E作EH⊥AB，垂足為H，
∵AE=AD+DC+CE=68，
∴EH=AEsin75°=68sin75°=68×0.97=65.96≈66（cm），
∴車座點E到車架檔AB的距離約是66cm．

點評 本題是解直角三角形的應用，考查了銳角三角函數的定義，根據題目已知特點選用適當銳角三角函數或邊角關系去解直角三角形即可．