
分析 根據一次函數的增減性,可知本題分兩種情況:①當k>0時,y隨x的增大而增大,把x=-2,y=-6;x=5,y=-3代入一次函數的解析式y=kx+b,運用待定系數法即可求出函數的解析式;②當k<0時,y隨x的增大而減小,把x=-2,y=-3;x=5,y=-6代入一次函數的解析式y=kx+b,運用待定系數法即可求出函數的解析式.
解答 解:分兩種情況:
①當k>0時,把x=-2,y=-6;x=5,y=-3代入一次函數的解析式y=kx+b,
得$\left\{\begin{array}{l}{-2k+b=-6}\\{\;}\\{5k+b=-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{3}{7}}\\{\;}\\{b=-\frac{36}{7}}\end{array}\right.$,
則這個函數的解析式是y=$\frac{3}{7}x-\frac{36}{7}$(-2≤x≤5);
②當k<0時,把x=-2,y=-3;x=5,y=-6代入一次函數的解析式y=kx+b,
得$\left\{\begin{array}{l}{-2k+b=-3}\\{\;}\\{5k+b=-6}\end{array}\right.$,
解得
$\left\{\begin{array}{l}{k=-\frac{3}{7}}\\{\;}\\{b=-\frac{27}{7}}\end{array}\right.$,
則這個函數的解析式是y=-$\frac{3}{7}$x-$\frac{27}{7}$(-2≤x≤5).
故這個函數的解析式為:y=$\frac{3}{7}x-\frac{36}{7}$(-2≤x≤5)或者y=-$\frac{3}{7}$x-$\frac{27}{7}$(-2≤x≤5).
故答案為:y=$\frac{3}{7}x-\frac{36}{7}$(-2≤x≤5)或y=-$\frac{3}{7}$x-$\frac{27}{7}$(-2≤x≤5).
點評 本題主要考查一次函數的性質,當k>0時,y隨x的增大而增大,當k<0時,y隨x的增大而減小,注意要分情況討論是解答此題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
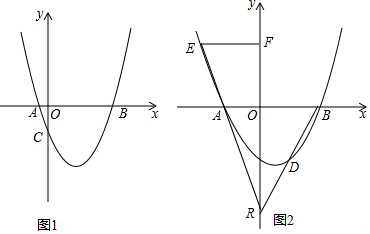
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 (1)解方程:x2-2x=2x+1
(1)解方程:x2-2x=2x+1查看答案和解析>>
科目:初中數學 來源: 題型:解答題
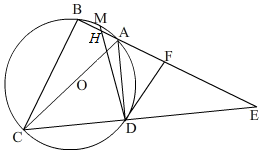 如圖,⊙O是四邊形ABCD的外接圓,AC是直徑,分別延長AB、CD相交于點E,AC=AE,過點D作DF∥BC于點F.
如圖,⊙O是四邊形ABCD的外接圓,AC是直徑,分別延長AB、CD相交于點E,AC=AE,過點D作DF∥BC于點F.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,小明在山腳下的A處測得山頂N的仰角為45°,此時,他剛好與山底D在同一水平線上.然后沿著坡度為30°的斜坡正對著山頂前行110米到達B處,測得山頂N的仰角為60°.求山的高度.(結果精確到1米,參考數據:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
如圖,小明在山腳下的A處測得山頂N的仰角為45°,此時,他剛好與山底D在同一水平線上.然后沿著坡度為30°的斜坡正對著山頂前行110米到達B處,測得山頂N的仰角為60°.求山的高度.(結果精確到1米,參考數據:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
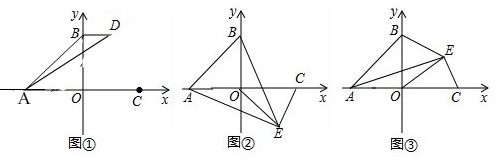
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com