
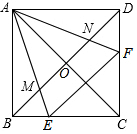
 如圖,點E,F分別為正方形ABCD的邊BC,CD上一點,AC,BD交于點O,且∠EAF=45°,AE,AF分別交對角線BD于點M,N,則有以下結論:①∠AEB=∠AEF=∠ANM;②EF=BE+DF;③△AOM∽△ADF;④S△AEF=2S△AMN
如圖,點E,F分別為正方形ABCD的邊BC,CD上一點,AC,BD交于點O,且∠EAF=45°,AE,AF分別交對角線BD于點M,N,則有以下結論:①∠AEB=∠AEF=∠ANM;②EF=BE+DF;③△AOM∽△ADF;④S△AEF=2S△AMN分析 如圖,把△ADF繞點A順時針旋轉90°得到△ABH,由旋轉的性質得,BH=DF,AH=AF,∠BAH=∠DAF,由已知條件得到∠EAH=∠EAF=45°,根據全等三角形的性質得到EH=EF,∴∠AEB=∠AEF,求得BE+BH=BE+DF=EF,故②正確;根據三角形的外角的性質得到∠ANM=∠AEB,于是得到∠AEB=∠AEF=∠ANM;故①正確;根據相似三角形的判定定理得到△OAM∽△DAF,故③正確;由△AMN∽△BME,得到$\frac{AM}{BM}=\frac{MN}{ME}$,推出△AMB∽△NME,根據相似三角形的性質得到∠AEN=∠ABD=45°,推出△AEN是等腰直角三角形,根據勾股定理得到AE=$\sqrt{2}$AN,根據相似三角形的性質得到EF=$\sqrt{2}$MN,于是得到S△AEF=2S△AMN故④正確.
解答 解:如圖,把△ADF繞點A順時針旋轉90°得到△ABH,
由旋轉的性質得,BH=DF,AH=AF,∠BAH=∠DAF,
∵∠EAF=45°,
∴∠EAH=∠BAH+∠BAE=∠DAF+∠BAE=90°-∠EAF=45°,
∴∠EAH=∠EAF=45°,
在△AEF和△AEH中,
$\left\{\begin{array}{l}{AH=AF}\\{∠EAH=∠EAF=45°}\\{AE=AE}\end{array}\right.$,
∴△AEF≌△AEH(SAS),
∴EH=EF,
∴∠AEB=∠AEF,
∴BE+BH=BE+DF=EF,故②正確;
∵∠ANM=∠ADB+∠DAN=45°+∠DAN,
∠AEB=90°-∠BAE=90°-(∠HAE-∠BAH)=90°-(45°-∠BAH)=45°+∠BAH,
∴∠ANM=∠AEB,
∴∠AEB=∠AEF=∠ANM;故①正確;
∵AC⊥BD,
∴∠AOM=∠ADF=90°,
∵∠MAO=45°-∠NAO,∠DAF=45°-∠NAO,
∴△OAM∽△DAF,故③正確;
連接NE,
∵∠MAN=∠MBE=45°,∠AMN=∠BME,
∴△AMN∽△BME,
∴$\frac{AM}{BM}=\frac{MN}{ME}$,
∴$\frac{AM}{MN}=\frac{BM}{ME}$,∵∠AMB=∠EMN,
∴△AMB∽△NME,
∴∠AEN=∠ABD=45°,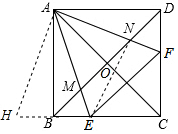
∵∠EAN=45°,
∴∠NAE=∠NEA=45°,
∴△AEN是等腰直角三角形,
∴AE=$\sqrt{2}$AN,
∵△AMN∽△BME,△AFE∽△BME,
∴△AMN∽△AFE,
∴$\frac{MN}{EF}=\frac{AN}{AE}$=$\frac{1}{\sqrt{2}}$,
∴EF=$\sqrt{2}$MN,
∵AB=$\sqrt{2}$AO,
∴S△AEF=S△AHE=$\frac{1}{2}$HE•AB=$\frac{1}{2}$EF•AB=$\frac{1}{2}$$•\sqrt{2}$MN$•\sqrt{2}$AO=2×$\frac{1}{2}$MN•AO=2S△AMN.故④正確.
故答案為:①②③④.
點評 本題考查了相似三角形的判定和性質,正方形的性質,全等三角形的判定與性質,等腰直角三角形的性質,勾股定理,熟記各性質并利用旋轉變換作輔助線構造成全等三角形是解題的關鍵.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:選擇題
| A. | 2x2y-xy2-(x2y-3xy2)=x2y+2xy2 | B. | $\sqrt{20}$-$\sqrt{5}$=$\sqrt{15}$ | ||
| C. | (2a2)3=8a6 | D. | -a2•3a=-3a3 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
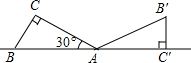 如圖所示,將一個含30°角的直角三角板ABC繞點A順時針旋轉,使得點B,A,C′在同一條直線上,若BC=1,則點B旋轉到B′所經過的路線長為$\frac{5}{3}$π.
如圖所示,將一個含30°角的直角三角板ABC繞點A順時針旋轉,使得點B,A,C′在同一條直線上,若BC=1,則點B旋轉到B′所經過的路線長為$\frac{5}{3}$π.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 將拋物線y=x2向左平移4個單位后,再向下平移2個單位,則此時拋物線的解析式是y=(x+4)2-2 | |
| B. | 方程x2+2x+3=0有兩個不相等的實數根 | |
| C. | 平行四邊形既是中心對稱圖形又是軸對稱圖形 | |
| D. | 平分弦的直徑垂直于弦,并且平分這條弦所對的兩條弧 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
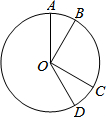 如圖,⊙O的半徑為3,點A,B,C,D都在⊙O上,∠AOB=30°,將扇形AOB繞點O順時針旋轉120°后恰好與扇形COD重合,則$\widehat{AD}$的長為$\frac{5}{2}$π.(結果保留π)
如圖,⊙O的半徑為3,點A,B,C,D都在⊙O上,∠AOB=30°,將扇形AOB繞點O順時針旋轉120°后恰好與扇形COD重合,則$\widehat{AD}$的長為$\frac{5}{2}$π.(結果保留π)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com