Question

12．如圖Rt△ABC，AB=AC=6，D為AC上一點，連接BD，AF⊥BD交BD于H，交BC于F，CE⊥AC交AF的延長線于E，
（1）求證：△ABD≌△CAE；
（2）當D為AC上離A點最近的三等分點時，連接DE，求DE的長；
（3）當D為AC上離A點最近的n等分點時，連接BE，求S_△BDC：S_△BEC（用含n的代數式表示，直接寫出答案）

Answer 1

分析 （1）先根據Rt△ABC中，∠BAD=90°，AH⊥BD，得到∠2=∠3，再根據∠ACE=∠BAD=90°，運用ASA判定△ABD≌△CAE即可；
（2）先根據全等三角形的性質得到CE=AD，再根據D為AC上離A點最近的三等分點，求得AD=2，CD=4，再根據CE=2，∠DCE=90°，運用勾股定理求得DE即可；
（3）根據全等三角形的性質得到CE=AD，再根據D為AC上離A點最近的n等分點，求得AD和CD，再根據AB=AC=6，求得S_△BDC和S_△BEC，最后計算其比值即可．

解答 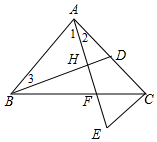解：（1）如圖1，Rt△ABC中，∠BAD=90°，AH⊥BD，
∴∠1+∠2=∠1+∠3=90°，
∴∠2=∠3，
又∵CE⊥AC，
∴∠ACE=∠BAD=90°，
在△ABD和△CAE中，
$\left\{\begin{array}{l}{∠BAD=∠ACE}\\{AB=CA}\\{∠3=∠2}\end{array}\right.$，
∴△ABD≌△CAE（ASA）；

（2）如圖2，∵△ABD≌△CAE，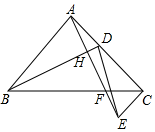
∴CE=AD，
∵D為AC上離A點最近的三等分點，AC=6，
∴AD=2，CD=4，
∴CE=2，
∵∠DCE=90°，
∴Rt△CDE中，DE=$\sqrt{C{D}^{2}+C{E}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$；

（3）如圖3，∵△ABD≌△CAE，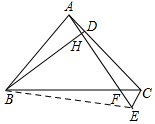
∴CE=AD，
∵D為AC上離A點最近的n等分點，AC=6，
∴AD=$\frac{6}{n}$，CD=6-$\frac{6}{n}$=$\frac{6（n-1）}{n}$，
∴CE=$\frac{6}{n}$，
∴S_△BDC=$\frac{1}{2}$×CD×AB=$\frac{1}{2}$×$\frac{6（n-1）}{n}$×6=$\frac{18（n-1）}{n}$，
S_△BEC=$\frac{1}{2}$×CE×AC=$\frac{1}{2}$×$\frac{6}{n}$×6=$\frac{18}{n}$，
∴S_△BDC：S_△BEC=$\frac{18（n-1）}{n}$：$\frac{18}{n}$=n-1．

點評 本題屬于三角形綜合題，主要考查了全等三角形的判定與性質、等腰直角三角形的性質以勾股定理的綜合應用，在應用全等三角形的判定時，要注意三角形間的公共邊和公共角，必要時添加適當輔助線構造三角形．