
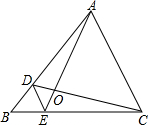
 如圖,D、E分別是△ABC的邊AB、BC上的點,DE∥AC,若S△BDE:S△CDE=1:3,求S△DOE:S△AOC的值.
如圖,D、E分別是△ABC的邊AB、BC上的點,DE∥AC,若S△BDE:S△CDE=1:3,求S△DOE:S△AOC的值. 分析 由已知得出BE:BC=1:4;證明△DOE∽△AOC,得到$\frac{DE}{AC}=\frac{1}{4}$,由相似三角形的性質即可解決問題.
解答 解:∵S△BDE:S△CDE=1:3,
∴BE:EC=1:3;
∴BE:BC=1:4;
∵DE∥AC,
∴△DOE∽△AOC,
∴$\frac{DE}{AC}=\frac{BE}{BC}$=$\frac{1}{4}$,
∴S△DOE:S△AOC=($\frac{1}{4}$)=$\frac{1}{16}$.
點評 本題主要考查了相似三角形的判定及其性質的應用問題;熟練掌握相似三角形的判定與性質,證出BE:BC=1:4是解決問題的關鍵解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 運輸工具 | 途中平均速度 (千米/時) | 運費 (元/千米) | 裝卸費用 (元) |
| 火車 | 100 | 15 | 2000 |
| 汽車 | 80 | 20 | 900 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 銷售單價(元) | x(x>30) |
| 銷售量y(件) | -10x+800 |
| 銷售玩具獲得利潤w(元) | -10x2+1000x-16000 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com