
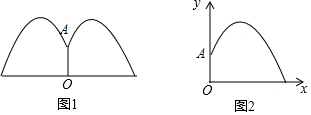 公園里有一個圓形噴水池,在水池中央垂直于水面安裝一個花形柱子OA,O恰好在水面中心,布置在柱子頂端A處的噴頭向外噴水,水流在各個方向上沿形狀相同的拋物線路徑落下,且在過OA任意平面上的拋物線如圖1所示,建立直角坐標系如圖2,水流噴出的高度(m)與水面距離x(m)之間的函數關系式是y=a(x-h)2+k,且OA=1.25m,水柱在離OA為1m處到時達最大高度2.25m,請回答下列問題:
公園里有一個圓形噴水池,在水池中央垂直于水面安裝一個花形柱子OA,O恰好在水面中心,布置在柱子頂端A處的噴頭向外噴水,水流在各個方向上沿形狀相同的拋物線路徑落下,且在過OA任意平面上的拋物線如圖1所示,建立直角坐標系如圖2,水流噴出的高度(m)與水面距離x(m)之間的函數關系式是y=a(x-h)2+k,且OA=1.25m,水柱在離OA為1m處到時達最大高度2.25m,請回答下列問題:分析 (1)根據已知得出二次函數的頂點坐標,即可利用頂點式得出二次函數解析式,令y=0,則-(x-1)2+2.25=0,求出x的值即可得出答案.;
(2)當水流噴出的拋物線形狀與(1)相同,即a=-1,當x=3.5時,y=0,進而求出答案即可.
解答 解:(1)∵頂點為(1,2.25),
∴設解析式為y=a(x-1)2+2.25過點(0,1.25),
解得a=-1,
所以解析式為:y=-(x-1)2+2.25,
令y=0,
則-(x-1)2+2.25=0,
解得x=2.5 或x=-0.5(舍去),
所以水池的半徑至少要2.5米才能使噴出的水流不致落到池外;
(2)由于噴出的拋物線形狀與(1)相同,可設此拋物線為y=-x2+bx+c,
把點(0,1.25)(3.5,0)
∴$\left\{\begin{array}{l}{c=1.25}\\{-\frac{49}{4}+\frac{7}{2}b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=\frac{22}{7}}\\{c=\frac{5}{4}}\end{array}\right.$,
∴y=-x2+$\frac{22}{7}$x+$\frac{5}{4}$=-(x-$\frac{11}{7}$)2+$\frac{729}{196}$,
∴水池的半徑為3.5m,要使水流不落到池外,此時水流最大高度應達$\frac{729}{196}$米.
點評 此題主要考查了二次函數的應用,根據頂點式求出二次函數的解析式是解題關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知實數a、b在數軸上的位置如圖所示,試化簡:$\frac{a}{a-b}$$\sqrt{\frac{{a}^{2}b-2a{b}^{2}+{b}^{3}}{a}}$.
已知實數a、b在數軸上的位置如圖所示,試化簡:$\frac{a}{a-b}$$\sqrt{\frac{{a}^{2}b-2a{b}^{2}+{b}^{3}}{a}}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com