
分析 (1)設該公司生產每件商品的成本為a元,根據:實際售價-成本=利潤,列出方程,解方程可得;
(2)根據:每天利潤=單件利潤×每天銷售量列出函數關系式,配方成頂點式可得函數的最值情況;
(3)根據(2)中每天利潤減去每天開支a元列出函數關系式P=-2(x-50)2+5000-a,根據最大利潤要控制在4000元至4500元之間可得關于a的不等式,解不等式可得a的取值范圍,再由至少有90天的盈利可知-2x2+200x-a=0的兩根x1、x2間距離x1-x2≥90,根據韋達定理可得關于a的不等式,求得a的范圍,綜合上述情況確定a的范圍.
解答 解:(1)設該公司生產每件商品的成本為m元,則
(1+20%)•m=0.8×(15+30)
解得,m=30,
即該公司生產每件商品的成本為30元;
(2)設銷售該商品第x天時,當天的利潤為w元,則
w=(200-2x)(x+30-30)=-2(x-50)2+5000,
∴當x=50時,w取得最大值,此時w=5000,
即銷售該商品第50天時,每天的利潤最大,最大利潤5000元;
(3)記公司每天控制人工、水電和房租支出共計a元后利潤為P,
則P=-2(x-50)2+5000-a,
根據題意:4000≤5000-a≤4500,
解得:500≤a≤1000,
又∵至少有90天的盈利,
∴-2x2+200x-a=0的兩根x1、x2間距離x1-x2≥90,
∴(x1-x2)2≥902,即(x1+x2)2-4x1x2≥902,
∵x1+x2=100,x1x2=$\frac{a}{2}$,
∴1002-4×$\frac{a}{2}$≥902,
解得:a≤950,
綜上,500≤a≤950.
點評 本題主要考查二次函數的實際應用能力,明確不等關系并據此列出方程或函數關系式是解題基礎,根據題意挖掘出不等關系求a的范圍是關鍵.


科目:初中數學 來源: 題型:解答題
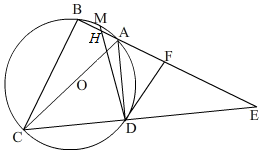 如圖,⊙O是四邊形ABCD的外接圓,AC是直徑,分別延長AB、CD相交于點E,AC=AE,過點D作DF∥BC于點F.
如圖,⊙O是四邊形ABCD的外接圓,AC是直徑,分別延長AB、CD相交于點E,AC=AE,過點D作DF∥BC于點F.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
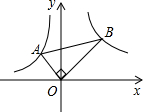 如圖,A、B分別為反比例函數y=-$\frac{2}{x}$(x<0),y=$\frac{8}{x}$(x>0)圖象上的點,且OA⊥OB,則sin∠ABO的值為( )
如圖,A、B分別為反比例函數y=-$\frac{2}{x}$(x<0),y=$\frac{8}{x}$(x>0)圖象上的點,且OA⊥OB,則sin∠ABO的值為( )| A. | $\frac{\sqrt{2}}{5}$ | B. | $\frac{\sqrt{3}}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{7}}{5}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
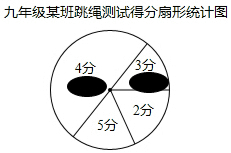 本學期開學初,學校體育組對九年級某班50名學生進行了跳繩項目的測試,根據測試成績制作了下面扇形統計圖,扇形統計圖中的部分數據已被涂黑,但知道以下信息:得4分人數比得3分人數4倍多5人;得2分人數與得5分人數一樣多,均為10人.
本學期開學初,學校體育組對九年級某班50名學生進行了跳繩項目的測試,根據測試成績制作了下面扇形統計圖,扇形統計圖中的部分數據已被涂黑,但知道以下信息:得4分人數比得3分人數4倍多5人;得2分人數與得5分人數一樣多,均為10人.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,在△ABC中,∠B=90°,AB=21,BC=20,有一個半徑為10的圓分別與AB、BC相切,則此圓的圓心是( )
如圖,在△ABC中,∠B=90°,AB=21,BC=20,有一個半徑為10的圓分別與AB、BC相切,則此圓的圓心是( )| A. | AB邊的中垂線與BC中垂線的交點 | B. | ∠B的平分線與AB的交點 | ||
| C. | ∠B的平分線與AB中垂線的交點 | D. | ∠B的平分線與BC中垂線的交點 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com