
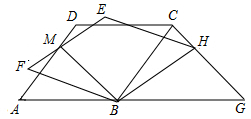
 如圖,菱形ABCD邊長為5,tan∠DAB=$\frac{4}{3}$,將菱形繞點B按順時針方向旋轉角α(0°<α<∠DBA)得到菱形FBHE(點A的對應點為點F),EF與AD交于點M,連接BM.
如圖,菱形ABCD邊長為5,tan∠DAB=$\frac{4}{3}$,將菱形繞點B按順時針方向旋轉角α(0°<α<∠DBA)得到菱形FBHE(點A的對應點為點F),EF與AD交于點M,連接BM.分析 (1)作輔助線,構建直角三角形,根據三角函數和菱形的邊長為5得:BP=4,AP=3,再求PM的長,利用勾股定理求BM的長;
(2)作輔助線,證明PB=BN,證△ABP≌△FBN;最后結合角平分線的性質證得結論;
(3)如圖2,過點M作MQ⊥AG于點Q,過C作CH⊥AG于點H,構建相似三角形△AMB∽△BCG,根據該相似三角形的對應邊成比例得到求得MQ的長度.結合已知條件tan∠DAB=$\frac{4}{3}$,來求邊AQ的長度,即可得到AM的長.
解答 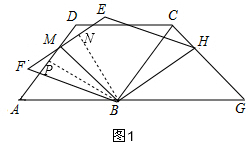 解:(1)如圖1,過點A作AM⊥OC于點M,
解:(1)如圖1,過點A作AM⊥OC于點M,
在直角△AOM中,∵tan∠DAB=$\frac{4}{3}$,OA=5,
∴BP=4,AP=3,
∵AM=4,
∴PM=AM-AP=4-3=1,
∴BM=$\sqrt{P{M}^{2}+B{P}^{2}}$=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$;
(2)如圖1,過點A作AN⊥EF于點N,
∵在△ABP與△FBN中,
$\left\{\begin{array}{l}{∠A=∠F}\\{∠APB=∠FNB=90°}\\{AB=BF}\end{array}\right.$,
∴△ABP≌△FBN(AAS),
∴BP=BN,
∴MB平分∠AME;
(3)如圖2,過點M作MQ⊥AG于點Q,過C作CH⊥AG于點H,
由旋轉可知:∠ABF=∠CBH=α,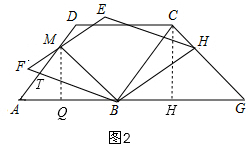
∵BC=BH,
∴∠BCH=$\frac{180°-α}{2}$,
∵∠A=∠F,∠ATB=∠MTF,
∴∠ABF=∠FMT=α,
由(2)得:∠AMB=∠BME=$\frac{180°-α}{2}$,
∴∠AMB=∠BCH,
又∵AD∥BC,
∴∠A=∠CBG,
∴△AMB∽△BCG,
∴$\frac{MQ}{CH}$=$\frac{AB}{BG}$,
∵AG=12,AB=5,
∴BG=12-5=7,
∴$\frac{MQ}{4}=\frac{5}{7}$,
∴MQ=$\frac{20}{7}$,
∵tan∠DAB=$\frac{4}{3}$=$\frac{MQ}{AQ}$,
∴AQ=3×$\frac{20}{7}$÷4=$\frac{15}{7}$,
由勾股定理得:AM=$\sqrt{A{Q}^{2}+M{Q}^{2}}$=$\sqrt{(\frac{15}{7})^{2}+(\frac{20}{7})^{2}}$=$\frac{25}{7}$.
點評 本題考查了四邊形綜合題.解題過程中,涉及到了全等三角形的判定與性質,相似三角形的判定與性質,旋轉的性質,解直角三角形以及勾股定理等知識點,解答該題的難點在于作出輔助線,構建相關的圖形的性質.


 期末寶典單元檢測分類復習卷系列答案
期末寶典單元檢測分類復習卷系列答案科目:初中數學 來源: 題型:選擇題
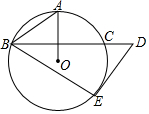 如圖,OA是⊙O的半徑,BC是⊙O的弦,且BC⊥OA,過BC的延長線上一點D作⊙O的切線DE,切點為E,連接AB,BE,若∠BDE=52°,則∠ABE的度數是( )
如圖,OA是⊙O的半徑,BC是⊙O的弦,且BC⊥OA,過BC的延長線上一點D作⊙O的切線DE,切點為E,連接AB,BE,若∠BDE=52°,則∠ABE的度數是( )| A. | 52° | B. | 58° | C. | 60° | D. | 64° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
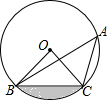 如圖,點A、B、C在⊙O上,若∠BAC=45°,OB=2,則圖中陰影部分的面積為( )
如圖,點A、B、C在⊙O上,若∠BAC=45°,OB=2,則圖中陰影部分的面積為( )| A. | π-2 | B. | $\frac{2}{3}π-1$ | C. | π-4 | D. | $\frac{2}{3}π-2$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com