
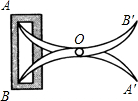
 如圖,將兩根鋼條AA′,BB′的中點O釘在一起,使AA′,BB′能繞點O自由轉動,就做成一個測量工具,測A′B′的長即等于內槽寬AB,這種測量方法的依據是兩邊和它們的夾角分別相等的兩個三角形全等,全等三角形的對應邊相等..
如圖,將兩根鋼條AA′,BB′的中點O釘在一起,使AA′,BB′能繞點O自由轉動,就做成一個測量工具,測A′B′的長即等于內槽寬AB,這種測量方法的依據是兩邊和它們的夾角分別相等的兩個三角形全等,全等三角形的對應邊相等.. 分析 由O是AA′、BB′的中點,可得AO=A′O,BO=B′O,再有∠AOA′=∠BOB′,可以根據全等三角形的判定方法SAS,判定△OAB≌△OA′B′,根據全等三角形的性質即可得到結論.
解答 解:∵O是AA′、BB′的中點,
∴AO=A′O,BO=B′O,
在△OAB和△OA′B′中$\left\{\begin{array}{l}{AO=A′O}\\{∠AOA′=∠BOB′}\\{BO=B′O}\end{array}\right.$,
∴△OAB≌△OA′B′(SAS),
∴AB=A′B′,
故兩邊和它們的夾角分別相等的兩個三角形全等,全等三角形的對應邊相等.
故答案為:兩邊和它們的夾角分別相等的兩個三角形全等,全等三角形的對應邊相等.
點評 此題主要全等三角形的應用,關鍵是掌握全等三角形的判定方法:SSS、SAS、ASA、AAS,HL,要證明兩個三角形全等,必須有對應邊相等這一條件.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | |
| 甲(件) | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
| 乙(件) | 1 | 0 | 2 | 1 | 1 | 0 | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
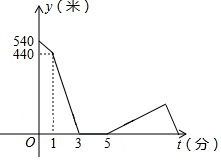 “歡樂跑中國•重慶站”比賽前夕,小剛和小強相約晨練跑步.小剛比小強早1分鐘跑步出門,3分鐘后他們相遇.兩人寒暄2分鐘后,決定進行跑步比賽.比賽時小剛的速度始終是180米/分,小強的速度是220米/分.比賽開始10分鐘后,因霧霾嚴重,小強突感身體不適,于是他按原路以出門時的速度返回,直到他們再次相遇.如圖所示是小剛、小強之間的距離y(千米)與小剛跑步所用時間x(分鐘)之間的函數圖象.問小剛從家出發到他們再次相遇時,一共用了$\frac{49}{3}$分鐘.
“歡樂跑中國•重慶站”比賽前夕,小剛和小強相約晨練跑步.小剛比小強早1分鐘跑步出門,3分鐘后他們相遇.兩人寒暄2分鐘后,決定進行跑步比賽.比賽時小剛的速度始終是180米/分,小強的速度是220米/分.比賽開始10分鐘后,因霧霾嚴重,小強突感身體不適,于是他按原路以出門時的速度返回,直到他們再次相遇.如圖所示是小剛、小強之間的距離y(千米)與小剛跑步所用時間x(分鐘)之間的函數圖象.問小剛從家出發到他們再次相遇時,一共用了$\frac{49}{3}$分鐘.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com