Question

12．如圖，點A、B的坐標分別是（0，4），（3，0），點C是線段AB的中點，動點P從點A出發，沿AO方向以每秒1個單位的速度向終點O運動，同時動點Q從O出發，以每秒2個單位的速度先沿OB方向運動到點B，再沿BA方向向終點A運動，以CP、CQ為鄰邊構造平行四邊形PCQD，設點P的運動時間為t秒．
（1）當t=1時，求CP的長；
（2）連接CD，當CD∥AP時，求t的值；
（3）當經過P、B、C三點的拋物線存在時，請直接寫出該拋物線頂點縱坐標的最值；
（4）連接OC，記運動過程中平行四邊形PCQD的面積為s，它與△AOC的重疊面積記為s₁，$\frac{{s}_{1}}{s}$＜$\frac{1}{3}$，請求出t的取值范圍．

Answer 1

分析 （1）求出點P坐標，利用兩點間距離公式計算即可．
（2）如圖2中，連接PB交CD于K．利用平行四邊形的性質可以證明，當Q與B重合時，CD∥PA，由此即可解決問題．
（3）設經過P、B、C三點的拋物線的解析式為y=ax²+bx+c，P（0，4-t），C（$\frac{3}{2}$，2），B（3，0）代入得到$\left\{\begin{array}{l}{c=4-t}\\{\frac{9}{4}a+\frac{3}{2}b+c=2}\\{9a+3b+c=0}\end{array}\right.$，可得拋物線的解析式為y=-$\frac{2}{9}$tx²+（t-$\frac{4}{3}$）x+4-t．推出拋物線頂點的縱坐標=$\frac{4×（-\frac{2}{9}t）（4-t）-（t-\frac{4}{3}）^{2}}{4×（-\frac{2}{9}t）}$=$\frac{1}{8}t+\frac{2}{t}$+1=$\frac{1}{8}$（$\sqrt{t}$-$\sqrt{\frac{16}{t}}$）²+2，由此即可解決問題．
（4）分四種情形討論即可①如圖3中，當線段PD與線段OC沒有交點時，重疊部分是四邊形PCKD，顯然不符合條件．②如圖4中，當線段PD與線段OC有交點時，設OC交PD于K，重疊部分是四邊形△PCK．③當點Q在線段BC上時，如圖6中，重疊部分是△PCK．④當點Q在線段AC上時，重疊部分是四邊形PCQK，由圖象可知，顯然不滿足條件．

解答 解：（1）如圖1中，

∵A（0，4），B（3，0），
∴OA=4，OB=3，AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5，
∵點C是線段AB的中點，
∴OC=AC=BC=$\frac{5}{2}$，C（$\frac{3}{2}$，2），
∵t=1，
∴AP=1，P（0，3），
∴PC=$\sqrt{{1}^{2}+（\frac{3}{2}）^{2}}$=$\frac{1}{2}$$\sqrt{13}$．

（2）如圖2中，連接PB交CD于K．

∵PC∥DQ，PD∥CQ，
∴四邊形PCQD是平行四邊形，
∴PK=KQ，
∴當Q與B重合時，點K的橫坐標為$\frac{0+3}{2}$=$\frac{3}{2}$，∵C（$\frac{3}{2}$，2），
∴CK∥AP，即CD∥PA，此時t=$\frac{3}{2}$s．

（3）設經過P、B、C三點的拋物線的解析式為y=ax²+bx+c，
把P（0，4-t），C（$\frac{3}{2}$，2），B（3，0）代入得到$\left\{\begin{array}{l}{c=4-t}\\{\frac{9}{4}a+\frac{3}{2}b+c=2}\\{9a+3b+c=0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{a=-\frac{2}{9}t}\\{b=t-\frac{4}{3}}\\{c=4-t}\end{array}\right.$，
∴拋物線的解析式為y=-$\frac{2}{9}$tx²+（t-$\frac{4}{3}$）x+4-t．
∴拋物線頂點的縱坐標=$\frac{4×（-\frac{2}{9}t）（4-t）-（t-\frac{4}{3}）^{2}}{4×（-\frac{2}{9}t）}$=$\frac{1}{8}t+\frac{2}{t}$+1=$\frac{1}{8}$（$\sqrt{t}$-$\sqrt{\frac{16}{t}}$）²+2，
∴當$\sqrt{t}$=$\sqrt{\frac{16}{t}}$時，拋物線頂點的縱坐標的最小值為2，
∴t=2時，拋物線頂點的縱坐標的最小值為2．

（4）①如圖3中，當線段PD與線段OC沒有交點時，重疊部分是四邊形PCKD，顯然不符合條件．

②如圖4中，當線段PD與線段OC有交點時，設OC交PD于K，重疊部分是四邊形△PCK．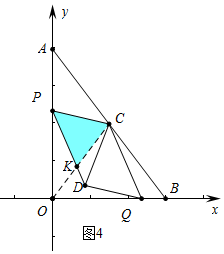

∵運動過程中平行四邊形PCQD的面積為s，它與△AOC的重疊面積記為s₁，$\frac{{s}_{1}}{s}$＜$\frac{1}{3}$，
∴當PK＜2KD時，$\frac{{s}_{1}}{s}$＜$\frac{1}{3}$，
當點Q與點B重合時，如圖5中，

∵PK∥AC，
∴$\frac{OP}{OA}$=$\frac{PK}{AC}$，
∴$\frac{2.5}{4}$=$\frac{PK}{AC}$，
∴PK=$\frac{5}{8}$AC=$\frac{5}{8}$BC=$\frac{5}{8}$PD，
∴PK=$\frac{5}{3}$KD，此時，$\frac{{s}_{1}}{s}$＜$\frac{1}{3}$，滿足條件．
如圖4中，∵P（0，4-t），C（$\frac{3}{2}$，2），Q（2t，0），設點D坐標為（m，n）則有$\frac{\frac{3}{2}+m}{2}$=$\frac{2t}{2}$，$\frac{2+n}{2}$=$\frac{4-t+0}{2}$，
∴m=2t-$\frac{3}{2}$，n=2-t，
∴D（2t-$\frac{3}{2}$，2-t），
∴直線CQ的解析式為y=$\frac{4}{3-4t}$x+$\frac{8t}{4t-3}$，
直線PD的解析式為y=$\frac{4}{3-4t}$x+4-t．
直線OC的解析式為y=$\frac{4}{3}$x，
由$\left\{\begin{array}{l}{y=\frac{4}{3}x}\\{y=\frac{4}{3-4t}x+4-t}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{3（t-4）（3-4t）}{16t}}\\{y=\frac{（t-4）（3-4t）}{4t}}\end{array}\right.$，
∴k（$\frac{3（t-4）（3-4t）}{16t}$，$\frac{（t-4）（3-4t）}{4t}$），
當PK=2KD時，PK：PD=2：3，
∴$\frac{3（t-4）（3-4t）}{16t}$：（2t-$\frac{3}{2}$）=2：3，
解得t=$\frac{36}{25}$，
∴當$\frac{36}{25}$＜t≤$\frac{3}{2}$時，$\frac{{s}_{1}}{s}$＜$\frac{1}{3}$，
③當點Q在線段BC上時，如圖6中，重疊部分是△PCK．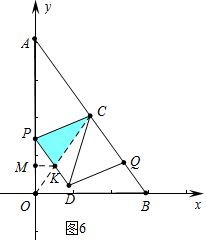

作KM⊥OP于M，
∵OC=AC=CB，
∴∠OCA=∠CAO，
∵PD∥AB，
∴∠KPO=∠CAO=∠KOP，
∴PK=KO，
∴PM=OM=$\frac{4-t}{2}$，
∵△PMK∽△AOB，
∴$\frac{PK}{AB}$=$\frac{PM}{OA}$，
∴$\frac{PK}{5}$=$\frac{\frac{4-t}{2}}{4}$，
∴PK=$\frac{5}{8}$（4-t），
∵PD=CQ=3+$\frac{5}{2}$-2t=$\frac{11}{2}$-2t，
當PK：PD=2：3時，
$\frac{5}{8}$（4-t）：（$\frac{11}{2}$-2t）=2：3，
解得t=$\frac{28}{17}$，
∴當$\frac{3}{2}$＜t＜$\frac{28}{17}$時，$\frac{{s}_{1}}{s}$＜$\frac{1}{3}$，
④當點Q在線段AC上時，重疊部分是四邊形PCQK，由圖象可知，顯然不滿足條件．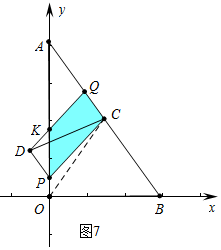

綜上所述，當$\frac{36}{25}$＜t＜$\frac{28}{17}$時，$\frac{{s}_{1}}{s}$＜$\frac{1}{3}$．

點評 本題考查二次函數綜合題、一次函數的應用、多邊形面積問題、相似三角形的判定和性質、平行四邊形的性質等知識，解題的關鍵是靈活運用所學知識解決問題，學會用分類討論的思想思考問題，注意不能漏解，學會利用配方法確定函數最值問題，屬于中考壓軸題．