Question

16．甲、乙兩輛汽車沿同一路線趕赴距出發地480千米的目的地，乙車比甲車晚出發2小時（從甲車出發時開始計時），圖中折線OABC，線段DE分別表示甲、乙兩車所行路程y（千米）與時間x（小時）之間的函數關系對應的圖象（線段AB表示甲出發不足2小時因故停車檢修），則當甲車出發$\frac{7}{3}$或$\frac{8}{3}$或$\frac{16}{3}$小時，甲、乙兩車相距80千米．

Answer 1

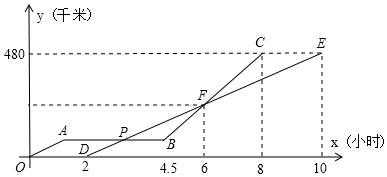
分析 先分別計算直線BC和DE的解析式，求出點P、F的坐標，根據圖形分三種情況討論，分別列方程可求得結論

解答 解：設DE的解析式為：y=kx+b，
把D（2，0），E（10，480）代入得：$\left\{\begin{array}{l}{2k+b=0}\\{10k+b=480}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=60}\\{b=-120}\end{array}\right.$，
∴DE的解析式為：y=60x-120，
當x=6時，y=60×6-120=240，
∴F（6，240），
設直線BC的解析式為：y=mx+n，
把F（6，240），C（8，480）代入得：$\left\{\begin{array}{l}{6m+n=240}\\{8m+n=480}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{m=120}\\{n=-480}\end{array}\right.$，
∴直線BC的解析式為：y=120x-480，
當x=4.5時，y=120×4.5-480=60，
當y=60時，60x-120=60，x=3
P（3，60）
因此在3小時前，甲、乙兩車不可能相距80千米，
分三種情況：
①當3＜x＜4.5時，60x-120-60=80，
x=$\frac{13}{3}$，
$\frac{13}{3}$-2=$\frac{7}{3}$，
②當4.5＜x＜6時，即在第二次相遇前，則60x-120-（120x-480）=80，
x=$\frac{14}{3}$，
$\frac{14}{3}$-2=$\frac{8}{3}$，
③當6＜x＜10時，即在第二次相遇后，則120x-480-（60x-120）=80，
x=$\frac{22}{3}$，
$\frac{22}{3}$-2=$\frac{16}{3}$，
答：則當甲車出發$\frac{7}{3}$或$\frac{8}{3}$或$\frac{16}{3}$小時，甲、乙兩車相距80千米；
故答案為：$\frac{7}{3}$或$\frac{8}{3}$或$\frac{16}{3}$．

點評 本題是一次函數的應用，屬于行程問題，考查了利用待定系數法求一次函數的解析式，并與行程問題的路程、時間、速度相結合，讀出圖形中的已知信息，是一道綜合性較強的題，有難度，同時也運用了數形結合的思想解決函數問題．