
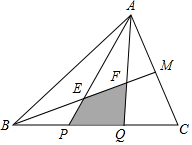
 如圖,S△ABC=1,AM=MC,BP=PQ=QC,求陰影部分的面積.
如圖,S△ABC=1,AM=MC,BP=PQ=QC,求陰影部分的面積. 分析 S△ABC=1、AM=MC、BP=PQ=QC知S△ABM=S△BCM=$\frac{1}{2}$S△ABC=$\frac{1}{2}$、S△APQ=S△ABP=S△AQC=$\frac{1}{3}$S△ABC=$\frac{1}{3}$,連接QM,知QM為△ACP的中位線,則AP=2MQ,MQ∥AP,從而得BE=EM、MQ=2EP,設BE=a,EP=b,則EM=a、MQ=2b、AP=4b,由AE∥MQ知$\frac{EF}{MF}=\frac{AE}{QM}$=$\frac{3b}{2b}=\frac{3}{2}$,從而得出EF=$\frac{3}{5}$a、FG=$\frac{2}{5}a$,則BE:EF:FG=a:$\frac{3}{5}$a:$\frac{2}{5}$a=5:3:2,繼而得出S△AEF=$\frac{3}{10}$S△ABM=$\frac{3}{10}$×$\frac{1}{2}$=$\frac{3}{20}$,根據S陰影=S△APQ-S△AEF可得答案.
解答 解:∵S△ABC=1,AM=MC,BP=PQ=QC,
∴S△ABM=S△BCM=$\frac{1}{2}$S△ABC=$\frac{1}{2}$,
S△APQ=S△ABP=S△AQC=$\frac{1}{3}$S△ABC=$\frac{1}{3}$,
連接QM,
∵PQ=QC,AM=CM,
∴QM為△ACP的中位線,
則AP=2MQ,MQ∥AP.
∵EP∥MQ,
∴$\frac{BE}{EM}=\frac{BP}{PQ}$=1,$\frac{EP}{MQ}=\frac{BP}{BQ}=\frac{1}{2}$,即BE=EM,MQ=2EP,
設BE=a,EP=b,
則EM=a,MQ=2b,AP=4b,
∴AE=3b,
∵AE∥MQ,
∴$\frac{EF}{MF}=\frac{AE}{QM}$=$\frac{3b}{2b}=\frac{3}{2}$,
∴EF=$\frac{3}{5}$a,FG=$\frac{2}{5}a$,
∴BE:EF:FG=a:$\frac{3}{5}$a:$\frac{2}{5}$a=5:3:2,
∴S△AEF=$\frac{3}{10}$S△ABM=$\frac{3}{10}$×$\frac{1}{2}$=$\frac{3}{20}$,
則S陰影=S△APQ-S△AEF=$\frac{1}{3}$-$\frac{3}{20}$=$\frac{11}{60}$.
點評 本題主要考查三角形的面積即平行線分線段成比例定理,熟練掌握等底共高時三角形面積間的關系及平行線分線段成比例定理是解題的關鍵.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 將一列整數1,2,3,-4,-5,-6,7,-8,-9,-10,…按如圖所示排列.如第一個頂峰的數是-6,第二個峰頂的數是15,那么第2016個峰頂的數是( )
將一列整數1,2,3,-4,-5,-6,7,-8,-9,-10,…按如圖所示排列.如第一個頂峰的數是-6,第二個峰頂的數是15,那么第2016個峰頂的數是( )| A. | 18150 | B. | -18150 | C. | 18141 | D. | -18141 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{a+b}{2}$ | B. | $\frac{a+b}{11}$ | C. | $\frac{5a+6b}{11}$ | D. | $\frac{1}{2}$($\frac{a}{5}$+$\frac{b}{6}$) |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com