
| A. | $\frac{1}{{2}^{4022}}$ | B. | $\frac{1}{{2}^{4024}}$ | C. | $\frac{1}{{2}^{4026}}$ | D. | $\frac{1}{{2}^{4028}}$ |
分析 由A2,B2,C2分別是△A1B1C1各邊的中點,根據三角形中位線的性質和有三組對應邊的比相等的兩個三角形相似得到△A2B2C2∽△A1B1C1,所以S△A2B2C2:S△A1B1C1=C2B22:C1B12=1:22,得到即S△A2B2C2=$\frac{1}{4}$,同理可得S△A3B3C3=$\frac{1}{4}$×$\frac{1}{4}$=($\frac{1}{4}$)2,以此類推即可得到第n個三角形的面積,據此進行計算即可.
解答 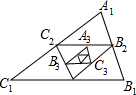 解:∵A2,B2,C2分別是△A1B1C1各邊的中點,
解:∵A2,B2,C2分別是△A1B1C1各邊的中點,
∴△A2B2C2∽△A1B1C1,
∴S△A2B2C2:S△A1B1C1=C2B22:C1B12=1:22,
即S△A2B2C2=$\frac{1}{4}$,
∴S△A3B3C3=$\frac{1}{4}$×$\frac{1}{4}$=($\frac{1}{4}$)2,
以此類推,第n個三角形的面積是($\frac{1}{4}$)n-1=($\frac{1}{2}$)2n-2,
∴第2014個三角形的面積為($\frac{1}{2}$)2×2014-2=$\frac{1}{{2}^{4026}}$.
故選:C.
點評 本題考查了三角形中位線定理以及三角形相似的性質的運用,解題的關鍵是找到問題的一般規律.


科目:初中數學 來源: 題型:解答題
 如圖,在邊長為1的小正方形組成的網格中,△ABC的頂點均在格點上,請按要求完成下列各題:
如圖,在邊長為1的小正方形組成的網格中,△ABC的頂點均在格點上,請按要求完成下列各題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
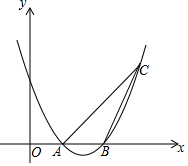 如圖,拋物線y=x2-4x+3與x軸交于A,B兩點,且過點C(4,3),在對稱軸右側的拋物線上是否存在點P,使∠PAC>∠ACB,若存在,求出點P的橫坐標xP的取值范圍;若不存在,請說明理由.
如圖,拋物線y=x2-4x+3與x軸交于A,B兩點,且過點C(4,3),在對稱軸右側的拋物線上是否存在點P,使∠PAC>∠ACB,若存在,求出點P的橫坐標xP的取值范圍;若不存在,請說明理由.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
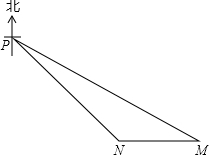 如圖,某海島上有一觀測點P,一天上午9:00觀測到一輪船在點M處,M在觀測點P南偏東60°方向上,漁船由東向西勻速航行跟蹤魚群,當天上午9:30漁船行至點N處,N在觀測點P的東南方向上,已知該漁船的速度為每小時40海里.
如圖,某海島上有一觀測點P,一天上午9:00觀測到一輪船在點M處,M在觀測點P南偏東60°方向上,漁船由東向西勻速航行跟蹤魚群,當天上午9:30漁船行至點N處,N在觀測點P的東南方向上,已知該漁船的速度為每小時40海里.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com