
分析 (1)根據有理化因式的定義,仿照閱讀中例子,得到$\sqrt{3}$、$\sqrt{2}$+1的有理化因式;
(2)利用分式的基本性質,分子和分母都乘以各自分母的有理化因式,化去分母中的根號.
解答 解:(1)因為$\sqrt{3}$×$\sqrt{3}$=3,所以$\sqrt{3}$的有理化因式是$\sqrt{3}$;
因為($\sqrt{2}+1$)($\sqrt{2}$-1)=3,所以$\sqrt{2}+1$的有理化因式是$\sqrt{2}$-1
故答案為:$\sqrt{3}$,$\sqrt{2}-1$
(2)$\frac{2}{\sqrt{5}}=\frac{2\sqrt{5}}{\sqrt{5}×\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,
$\frac{3}{3+\sqrt{6}}=\frac{3(3-\sqrt{6})}{(3+\sqrt{6})(3-\sqrt{6})}$
=3-$\sqrt{6}$
故答案為:$\frac{2\sqrt{5}}{5}$,3-$\sqrt{6}$
點評 本題考查了分母有理化的定義以及如何利用有理化因式化去分母中的根號.一般來說,$\sqrt{a}$,b$\sqrt{a}$,($\sqrt{a}$$+\sqrt{b}$)的有理化因式分別是$\sqrt{a}$,$\sqrt{a}$,($\sqrt{a}$$-\sqrt{b}$).


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源:2016-2017學年四川省眉山市第九年級下學期第一次月考數學試卷(解析版) 題型:填空題
關于x的一元二次方程(m-1)x2+x+m2-1=0的一個根為0,則m的值為__________
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
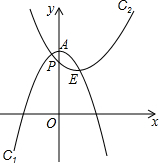 如圖,點A、點E的坐標分別為 (0,3)與(1,2),以點A為頂點的拋物線記為C1:y1=-x2+n;以E為頂點的拋物線記為C2:y2=ax2+bx+c,且拋物線C2與y軸交于點P(0,$\frac{5}{2}$).
如圖,點A、點E的坐標分別為 (0,3)與(1,2),以點A為頂點的拋物線記為C1:y1=-x2+n;以E為頂點的拋物線記為C2:y2=ax2+bx+c,且拋物線C2與y軸交于點P(0,$\frac{5}{2}$).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
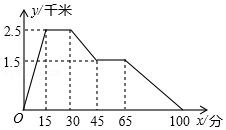 如圖反映的是小華從家里跑步去體育館,在那里鍛煉了一陣后又走到文具店去買筆,然后走回家,其中x表示時間,y表示小華離家的距離.根據圖象回答下列問題:
如圖反映的是小華從家里跑步去體育館,在那里鍛煉了一陣后又走到文具店去買筆,然后走回家,其中x表示時間,y表示小華離家的距離.根據圖象回答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com