
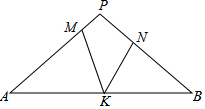
 如圖,在△PAB中,PA=PB,M,N,K分別是PA,PB,AB上的點,且AM=BK,BN=AK,若∠MKN=42°,則∠P的度數為( )
如圖,在△PAB中,PA=PB,M,N,K分別是PA,PB,AB上的點,且AM=BK,BN=AK,若∠MKN=42°,則∠P的度數為( )| A. | 44° | B. | 66° | C. | 96° | D. | 92° |
分析 根據等腰三角形的性質得到∠A=∠B,證明△AMK≌△BKN,得到∠AMK=∠BKN,根據三角形的外角的性質求出∠A=∠MKN=42°,根據三角形內角和定理計算即可.
解答 解:∵PA=PB,
∴∠A=∠B,
在△AMK和△BKN中,
$\left\{\begin{array}{l}{AM=BK}\\{∠A=∠B}\\{AK=BN}\end{array}\right.$,
∴△AMK≌△BKN,
∴∠AMK=∠BKN,
∵∠MKB=∠MKN+∠NKB=∠A+∠AMK,
∴∠A=∠MKN=42°,
∴∠P=180°-∠A-∠B=96°,
故選:C.
點評 本題考查的是等腰三角形的性質、全等三角形的判定和性質、三角形的外角的性質,掌握等邊對等角、全等三角形的判定定理和性質定理、三角形的外角的性質是解題的關鍵.


科目:初中數學 來源: 題型:解答題
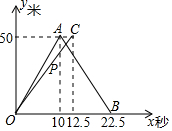 甲、乙兩人在相鄰兩條直跑道上進行競走比賽(注:跑道長50米,兩人均往返一次,返回時轉身的時間忽略不計),圖中的折線OA-AB是甲離出發點的距離y(米)與比賽時間x(秒)的函數圖象;線段OC是乙離出發點的距離y(米)與比賽時間x(秒)的函數圖象,其中x≥0,線段OC與AB相交于點P.根據圖象,解決下列問題:
甲、乙兩人在相鄰兩條直跑道上進行競走比賽(注:跑道長50米,兩人均往返一次,返回時轉身的時間忽略不計),圖中的折線OA-AB是甲離出發點的距離y(米)與比賽時間x(秒)的函數圖象;線段OC是乙離出發點的距離y(米)與比賽時間x(秒)的函數圖象,其中x≥0,線段OC與AB相交于點P.根據圖象,解決下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
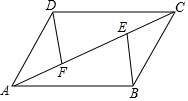 如圖,E,F是四邊形ABCD的對角線AC上點,AF=CE,DF=BE,DF∥BE.
如圖,E,F是四邊形ABCD的對角線AC上點,AF=CE,DF=BE,DF∥BE.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
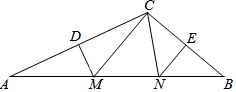 如圖,在△ABC中,DM、EN分別垂直平分AC和BC,交AB于M、N,
如圖,在△ABC中,DM、EN分別垂直平分AC和BC,交AB于M、N,查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2,4,2$\sqrt{3}$ | B. | 1,1,$\sqrt{2}$ | C. | 1,2,$\sqrt{5}$ | D. | $\sqrt{3}$,2,$\sqrt{5}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{\frac{1}{5}}$ | B. | $\sqrt{7}$ | C. | $\sqrt{24}$ | D. | $\frac{1}{{\sqrt{2}}}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com