
| A. | (2,0) | B. | (4,0) | C. | (-2,0) | D. | (0,0) |
分析 作A關于x軸的對稱點C,連接BC交x軸于P,連接AP,此時點P到點A和點B的距離之和最小,先求出C的坐標,設直線CB的解析式是y=kx+b,把C、B的坐標代入求出解析式是y=x-2,把y=0代入求出x即可.
解答 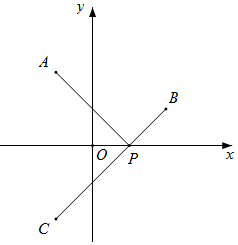 解:作A關于x軸的對稱點C,連接BC交x軸于P,連接AP,則此時AP+PB最小,
解:作A關于x軸的對稱點C,連接BC交x軸于P,連接AP,則此時AP+PB最小,
即此時點P到點A和點B的距離之和最小,
∵A(-2,4),
∴C(-2,-4),
設直線CB的解析式是y=kx+b,
把C、B的坐標代入得:
$\left\{\begin{array}{l}{2=4k+b\\;}\\{-4=-2k+b}\end{array}\right.$,
解得:k=1,b=-2,
∴y=x-2,
把y=0代入得:0=x-2,
解得x=2,
即P的坐標是(2,0),
故選A.
點評 本題考查了軸對稱-最短路線問題,一次函數的解析式,坐標與圖形性質等知識點的運用,解題的關鍵是根據軸對稱的性質畫出P的位置.凡是涉及最短距離的問題,一般要考慮線段的性質定理,多數情況要作點關于某直線的對稱點.


 學而優銜接教材南京大學出版社系列答案
學而優銜接教材南京大學出版社系列答案 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:初中數學 來源: 題型:選擇題
| A. | (a+b)2=a2+b2 | B. | (b-a)2=b2-2ab+a2 | C. | (a+2b)(a-2b)=a2-2b2 | D. | (a-b)2=a2-2ab-b2 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
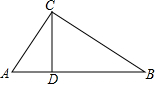 如圖,在△ABC中,∠ACB=90°,CD⊥AB于點D,已知BC=a,∠A=α,則下列結論錯誤的是( )
如圖,在△ABC中,∠ACB=90°,CD⊥AB于點D,已知BC=a,∠A=α,則下列結論錯誤的是( )| A. | BD=a•sinα | B. | AD=$\frac{a•sinα}{tanα}$ | C. | AC=$\frac{a}{sinα}$ | D. | CD=a•cosα |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | a2b-2a3=a(ab-2a2) | B. | x2-x+$\frac{1}{4}$=${(x-\frac{1}{2})}^{2}$ | C. | x2+2x+1=x(x+2)+1 | D. | 4x2-y2=(4x+y)(4x-y) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
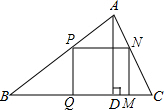 如圖,△ABC是一塊銳角三角形余料,邊BC=12厘米,高AD=8厘米,要把它加工成矩形零件PQMN,使矩形的一邊在BC上,其余兩個頂點分別在AB、AC上
如圖,△ABC是一塊銳角三角形余料,邊BC=12厘米,高AD=8厘米,要把它加工成矩形零件PQMN,使矩形的一邊在BC上,其余兩個頂點分別在AB、AC上查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com