
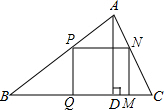
 如圖,△ABC是一塊銳角三角形余料,邊BC=12厘米,高AD=8厘米,要把它加工成矩形零件PQMN,使矩形的一邊在BC上,其余兩個頂點分別在AB、AC上
如圖,△ABC是一塊銳角三角形余料,邊BC=12厘米,高AD=8厘米,要把它加工成矩形零件PQMN,使矩形的一邊在BC上,其余兩個頂點分別在AB、AC上分析 (1)當PN=PQ時,矩形PQMN是正方形,設PN長為x厘米,由正方形的性質得出PN∥BC,PQ∥AD,根據平行線的性質,可以得出比例關系式$\frac{PQ}{AD}$=$\frac{BP}{AB}$、$\frac{PN}{BC}$=$\frac{AP}{AB}$,代入數據求解即可;
(2)先證明△APN∽△ABC,再根據相似三角形對應邊的比等于對應高的比列出比例式,即可求解;
(3)根據矩形面積公式得到關于x的二次函數,根據二次函數求出矩形的最大值.
解答 解:(1)∵PN=PQ,
∴矩形PQMN為正方形,
∴PN∥BC,PQ∥AD,
根據平行線的性質可以得出:$\frac{PQ}{AD}$=$\frac{BP}{AB}$、$\frac{PN}{BC}$=$\frac{AP}{AB}$,
設PN長為x厘米,則PQ=x,BC=12,AD=8,PN=x,
即$\frac{x}{8}$=$\frac{BP}{AB}$、$\frac{x}{12}$=$\frac{AP}{AB}$,
∵AP+BP=AB,
∴$\frac{x}{8}$+$\frac{x}{12}$=$\frac{BP}{AB}$+$\frac{AP}{AB}$=1,
解得x=$\frac{24}{5}$.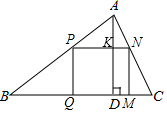 答:當PN=PQ時,PN的長度是$\frac{24}{5}$厘米;
答:當PN=PQ時,PN的長度是$\frac{24}{5}$厘米;
(2)設PN的長度是x厘米,PQ的長度是y厘米時,
∵四邊形PQMN為矩形,
∴BC∥PN,
∴△APN∽△ABC,
∴$\frac{PN}{BC}$=$\frac{AK}{AD}$,$\frac{x}{12}$=$\frac{8-y}{8}$,
∴y與x之間的函數關系式為y=8-$\frac{2}{3}$x(0<x<12);
(3)矩形PQMN面積=xy=x(8-$\frac{2}{3}$x)=-$\frac{2}{3}$x2+8x=-$\frac{2}{3}$(x-6)2+24,
故當PN的長度是6厘米時,矩形零件PQMN的面積最大,最大面積為24平方厘米.
點評 本題考查的是相似三角形的應用,利用矩形的面積公式得到關于x的二次函數,根據二次函數的性質,確定x的取值和面積的最大值是解題關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:選擇題
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| 日期 | 1號 | 2號 | 3號 | 4號 | 5號 | 6號 | 7號 |
| 空氣質量指數 | 446 | 402 | 456 | 499 | 500 | 434 | 105 |
| A. | 446,416 | B. | 446,406 | C. | 451,406 | D. | 499,416 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (2,0) | B. | (4,0) | C. | (-2,0) | D. | (0,0) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com