
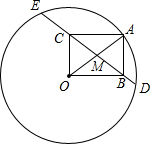
 如圖,⊙O的半徑為10,A是⊙O上一點.以OA為對角線作矩形OBAC,且OC=6.延長BC,與⊙O分別交于D,E兩點,則△OCE和△OBD的周長差等于( )
如圖,⊙O的半徑為10,A是⊙O上一點.以OA為對角線作矩形OBAC,且OC=6.延長BC,與⊙O分別交于D,E兩點,則△OCE和△OBD的周長差等于( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | 1 | D. | $\frac{6}{5}$ |
分析 連接OE、OD,作OF⊥DE于F,根據勾股定理求出OB,根據射影定理求出CF,得到BF,根據三角形的周長公式計算即可.
解答 解: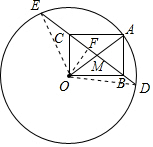 連接OE、OD,作OF⊥DE于F,
連接OE、OD,作OF⊥DE于F,
∵OC=AB=6,OA=10,
∴AC=OB=8,
∵四邊形ABOC是矩形,
∴BC=OA=10,
由射影定理得,OC2=CF•CB,
∴CF=$\frac{18}{5}$,
則BF=BC-CF=$\frac{32}{5}$,
∴CE-BD=$\frac{14}{5}$,又OB-OC=2,
∴△OCE的周長-△OBD的周長=(OE+OC+CE)-(OD+BD+OB)=$\frac{4}{5}$,
故選:B.
點評 本題考查的是垂徑定理、勾股定理和矩形的性質定理的應用,掌握垂直弦的直徑平分這條弦,并且平分弦所對的兩條弧是解題的關鍵.


 名師點撥卷系列答案
名師點撥卷系列答案 英才計劃期末調研系列答案
英才計劃期末調研系列答案科目:初中數學 來源:2016-2017學年北京市西城區七年級上學期期末考試數學試卷(解析版) 題型:解答題
A,B兩點在數軸上的位置如圖所示,其中點A對應的有理數為-4,且AB=10。動點P從點A出發,以每秒2個單位長度的速度沿數軸正方向運動,設運動時間為t秒(t>0)。

(1)當t=1時,AP的長為_________,點P表示的有理數為______;
(2)當PB=2時,求t的值;
(3)M為線段AP的中點,N為線段PB的中點. 在點P運動的過程中,線段MN的長度是否發生變化?若變化,請說明理由;若不變,請你畫出圖形,并求出線段MN的長。
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 6÷(-$\frac{1}{4}$)×4=6×(-4)×4 | B. | 6÷(-$\frac{1}{4}$)×4=6×(-$\frac{1}{4}$)×4 | C. | 6÷(-$\frac{1}{4}$)×4=6÷(-$\frac{1}{4}$×4) | D. | 6÷(-$\frac{1}{4}$)×4=6×(-4)÷4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,⊙O是△ABC的內切圓,點D,E,F為切點.
如圖,⊙O是△ABC的內切圓,點D,E,F為切點.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 有兩個內角是60°的三角形 | |
| B. | 有兩邊相等且是軸對稱圖形的三角形 | |
| C. | 三邊都相等的三角形 | |
| D. | 有一個角是60°且是軸對稱圖形的三角形 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在△ABC中,∠ACB=90°,AC=BC,點D為AB中點,點E在BA的延長線上,過B作BF⊥EC交EC延長線于F,交DC延長線于G.
如圖,在△ABC中,∠ACB=90°,AC=BC,點D為AB中點,點E在BA的延長線上,過B作BF⊥EC交EC延長線于F,交DC延長線于G.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (a+1)(a-1)=a2-1 | B. | x2-4=(x+2)(x-2) | ||
| C. | x2-4+3x=(x+2)(x-2)+3x | D. | x2-1=x(x-$\frac{1}{x}$) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com