

分析 (1)由矩形的四個角為直角,得到∠ABC為直角,再由BG垂直于AC,AE垂直于EF,得到一對直角相等,利用同角的余角相等得到一對角相等,再利用外角性質得到另一對角相等,利用兩角相等的三角形相似即可得證;
(2)延長BG,交AD于點K,利用兩角相等的三角形相似得到三角形ABK與三角形ABC相似,由相似得比例求出AK的長,由AK與BE平行,得到三角形AHK與三角形BHE相似,表示出EH,由第一問的結論,利用相似三角形對應邊成比例表示出$\frac{AH}{EM}$,即可確定出y與x的函數解析式,并求出定義域即可;
(3)當△BHE為等腰三角形時,分三種情況考慮:①當BH=BE時,利用等腰三角形的性質,角平分線定義及銳角三角函數定義求出BE的長;②當HB=HE時,利用等腰三角形的性質及銳角三角函數定義求出BE的長;③當EB=EH時,利用等腰三角形的性質及勾股定理求出BE的長即可.
解答 (1)證明:∵四邊形ABCD是矩形,
∴∠ABC=90°,即∠ABG+∠CBG=90°,
∵EF⊥AE,BG⊥AC,
∴∠AEF=∠BGA=90°,
∴∠AEF=∠ABC,∠ACB+∠CBG=90°,
∴∠ABG=∠ACB,
∵∠AEC=∠ABC+∠BAE,即∠AEF+∠CEF=∠ABC+∠BAE,
∴∠BAE=∠CEF,
又∵∠ABG=∠ACB,
∴△ABH∽△ECM;
(2)解:延長BG交AD于點K,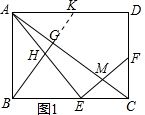
∵∠ABG=∠ACB,
又∵在矩形ABCD中,∠BAK=∠ABC=90°,
∴△ABK∽△BCA,
∴$\frac{AK}{AB}$=$\frac{AB}{BC}$,即$\frac{AK}{6}$=$\frac{6}{8}$,
∴AK=$\frac{9}{2}$,
∵在矩形ABCD中,AD∥BC,且BE=x,
∴$\frac{BE}{AK}$=$\frac{EH}{AH}$=$\frac{2x}{9}$,
∴EH=$\frac{2x}{9}$•AH,
∵△ABH∽△ECM,
∴$\frac{AH}{EM}$=$\frac{AB}{EC}$=$\frac{6}{8-x}$,
∵$\frac{EH}{EM}$=y,
∴y=$\frac{\frac{2x}{9}•AH}{EM}$=$\frac{2x}{9}$•$\frac{AH}{EM}$=$\frac{2x}{9}$•$\frac{6}{8-x}$=$\frac{4x}{24-3x}$(0<x<8);
(3)解:當△BHE為等腰三角形時,存在以下三種情況:
①當BH=BE時,則有∠BHE=∠BEH,
∵∠BHE=∠AHG,
∴∠BEH=∠AHG,
∵∠ABC=∠BGA=90°,
∴∠BEH+∠BAE=∠AHG+∠EAM=90°,
∴∠BAE=∠EAM,即AE為∠BAC的平分線,
過點E作EQ⊥AC,垂足為Q,如圖2所示,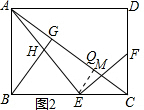
則EQ=EB=x,CE=8-x,
∵sin∠ACB=$\frac{EQ}{EC}$=$\frac{x}{8-x}$=$\frac{3}{5}$,
∴x=3,即BE=3;
②當HB=HE時,則有∠HBE=∠HEB,
∵∠ABC=∠BGC=90°,
∴∠BAE+∠HEB=∠BCG+∠HBE=90°,
∴∠BAE=∠BCG,
∴tan∠BAE=tan∠BCA=$\frac{x}{6}$=$\frac{3}{4}$,
∴x=$\frac{9}{2}$,即BE=$\frac{9}{2}$;
③當EB=EH時,則有∠EHB=∠EBH,
又∵∠EHB=∠AHG,
∴∠AHG=∠EBH,
∵∠BGA=∠BGC=90°,
∴∠CAE+∠AHG=∠BCG+∠EBH=90°,
∴∠CAE=∠BCG,
∴EA=EC=8-x,
∵在Rt△ABE中,AB2+BE2=AE2,即62+x2=(8-x)2,
解得:x=$\frac{7}{4}$,即BE=$\frac{7}{4}$,
綜上所述,當△BHE是等腰三角形時,BE的長為3或$\frac{9}{2}$或$\frac{7}{4}$.
點評 此題屬于相似形綜合題,涉及的知識有:矩形的性質,相似三角形的判定與性質,平行線等分線段定理,勾股定理,銳角三角函數定義,以及等腰三角形的性質,熟練掌握相似三角形的判定與性質是解本題的關鍵.


 全優考典單元檢測卷及歸類總復習系列答案
全優考典單元檢測卷及歸類總復習系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | y=$\sqrt{x-2}$ | B. | y=$\frac{1}{\sqrt{x-2}}$ | C. | y=$\sqrt{2x-1}$ | D. | y=$\frac{1}{\sqrt{2x-1}}$ |
查看答案和解析>>
科目:初中數學 來源:2017屆湖北省襄陽老河口九年級3月月考數學試卷(解析版) 題型:判斷題
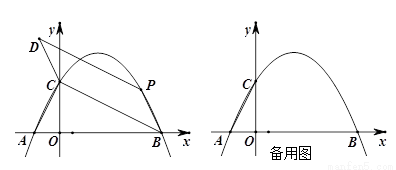
如圖,拋物線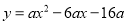 (
(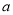 <0)與
<0)與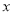 軸交于A,B兩點,與y軸正半軸交于點C,且∠ACB=90°,點P是直線BC上方拋物線上的一個動點.
軸交于A,B兩點,與y軸正半軸交于點C,且∠ACB=90°,點P是直線BC上方拋物線上的一個動點.
(1)請直接寫出A,B,C三點的坐標及拋物線的解析式;
(2)連接PB,以BP,BC為一組鄰邊作平行四邊形BCDP,當平行四邊形BCDP的面積最大時,求P,D兩點的坐標;
(3)若點Q是x 軸上一動點,是否存在以P,C,Q為頂點的三角形為等腰直角三角形?若存在,請直接寫出P,Q兩點的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com