
(本題14分)如圖,拋物線 與
與 軸相交于
軸相交于 、
、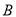 兩點(點
兩點(點 在點
在點 的左側),與
的左側),與 軸交于點
軸交于點 ,頂點為
,頂點為 .
.


(1)求出 、
、 兩點的坐標和拋物線的對稱軸;
兩點的坐標和拋物線的對稱軸;
(2)連接 ,與拋物線的對稱軸交于點
,與拋物線的對稱軸交于點 ,點
,點 為線段
為線段 上的一個動點,過點
上的一個動點,過點 作
作 交拋物線于點
交拋物線于點 ,設點
,設點 的橫坐標為
的橫坐標為 ;
;
①用含 的代數式表示線段
的代數式表示線段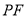 的長,并求出當
的長,并求出當 為何值時,四邊形
為何值時,四邊形 為平行四邊形?
為平行四邊形?
②設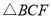 的面積為
的面積為 ,求
,求 與
與 的函數關系式.
的函數關系式.
(3)若點G為拋物線上的一個動點,在x軸上是否存在這樣的點H,使以B、C、G、H為頂點的四邊形是平行四邊形?如果存在,直接寫出滿足條件的H點的坐標;如果不存在,請說明理由.
(1)B(3,0),C(0,3),拋物線的對稱軸是x=1;
(2)①當m=2時,四邊形PEDF為平行四邊形;②S= (0≤m≤3).
(0≤m≤3).
(3)H坐標為H1(1,0)或H2(5,0)或H3( ,0)m的變化范圍是0≤m≤3
,0)m的變化范圍是0≤m≤3
【解析】
試題分析:(1)令y=0,則﹣x2+2x+3=﹣(x+1)(x﹣3)=0,
解得,x=﹣1或x=3,則A(﹣1,0),B(3,0).
所以,對稱軸是x= =1.
=1.
令x=0,則y=0,則C(0,3).
綜上所述, B(3,0),C(0,3),拋物線的對稱軸是x=1;
(2)①設直線BC的函數關系式為:y=kx+b(k≠0).
把B(3,0),C(0,3)分別代入得: ,
,
解得:k=﹣1,b=3.
所以直線BC的函數關系式為:y=﹣x+3.
當x=1時,y=﹣1+3=2,
∴E(1,2).
當x=m時,y=﹣m+3,
∴P(m,﹣m+3).
在y=﹣x2+2x+3中,當x=1時,y=4.
∴D(1,4)
當x=m時,y=﹣m2+2m+3,
∴F(m,﹣m2+2m+3)
∴線段DE=4﹣2=2,
線段PF=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m
∵PF∥DE,
∴當PF=ED時,四邊形PEDF為平行四邊形.
由﹣m2+3m=2,解得:m1=2,m2=1(不合題意,舍去).
因此,當m=2時,四邊形PEDF為平行四邊形.
②設直線PF與x軸交于點M,由B(3,0),O(0,0),可得:OB=OM+MB=3.
 =
= .
.
m的變化范圍是0≤m≤3.
(3)若以B、C、G、H為頂點的四邊形是平行四邊形,
①BH為四邊形的邊,則CG//BH
故點G和點C關于直線x=1對稱
∴G(2,3)且CG=2
此時BH=2
∴H1(1,0)或H2(5,0)
②BH為對角線,則此時G的縱坐標為-3
∴﹣x2+2x+3=-3,可得x= .有圖象可知x=
.有圖象可知x= 舍去
舍去
故G(3,  )
)
B、H關于點( ,0)
,0)
所以H( ,0)
,0)
綜上,H坐標為H1(1,0)或H2(5,0)或H3( ,0)
,0)
考點:拋物線的綜合運用


科目:初中數學 來源: 題型:
| k |
| x |
A、2
| ||
B、±2
| ||
C、
| ||
D、±
|
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省杭州市聯盟學校九年級上學期期中考試數學試卷(解析版) 題型:選擇題
如圖,⊙O的半徑OD⊥弦AB于點C,連結AO并延長交⊙O于點E,連結EC.若AB=8,CD=2,則EC的長為( )

A. B.8 C.
B.8 C. D.
D.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省杭州市蕭山地區九年級上學期期中考試數學試卷(解析版) 題型:選擇題
已知A,B,C是⊙O上不同的三個點,∠AOB=60°,則∠ACB=( )
A.60° B.30° C.60°或120° D.30°或150°
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省杭州市蕭山地區九年級上學期期中考試數學試卷(解析版) 題型:填空題
如圖,將弧BC 沿弦BC折疊交直徑AB于點D,若AD=5,DB=7,則BC的長是 .

查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省九年級上學期第二次月考數學試卷(解析版) 題型:選擇題
如圖,函數 的圖象與x軸的一個交點坐標為(3,0),則另一交點的橫坐標為( )
的圖象與x軸的一個交點坐標為(3,0),則另一交點的橫坐標為( )

A.-4 B.-3 C.-2 D.-1
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省九年級上學期第二次月考數學試卷(解析版) 題型:解答題
(本題8分)在梯形ABCD中,AD//BC,連結AC,且AC=BC,在對角線AC上取點E,使CE=AD,連接BE.

(1)求證:△DAC≌△ECB;
(2)若CA平分∠BCD,且AD=3,求BE的長.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省杭州市蕭山區高橋教育九年級上學期第二次檢測數學試卷(解析版) 題型:解答題
(本小題滿分10分)某經銷店為某工廠代銷一種建筑材料.當每噸售價為260元時,月銷售量為45噸.該經銷店為提高經營利潤,準備采取降價的方式進行促銷.經市場調查發現:當每噸售價每下降10元時,月銷售量就會增加7. 5噸.綜合考慮各種因素,每售出一噸建筑材料共需支付廠家及其它費用100元.設每噸材料售價為x(元),該經銷店的月利潤為y(元).
(1)當每噸售價是240元時,計算此時的月銷售量;
(2)求出y與x的函數關系式(不要求寫出x的取值范圍);
(3)該經銷店要獲得最大月利潤,售價應定為每噸多少元?
(4)小靜說:“當月利潤最大時,月銷售額也最大.”你認為對嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省金華市新世紀學校八年級上學期期中數學試卷(解析版) 題型:填空題
已知△ABC中,∠A:∠B:∠C=1:1:2,則這個三角形是 三角形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com