
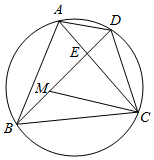
 如圖,點D是等邊三角形ABC外接圓上一點.M是BD上一點,且滿足DM=DC,點E是AC與BD的交點.
如圖,點D是等邊三角形ABC外接圓上一點.M是BD上一點,且滿足DM=DC,點E是AC與BD的交點.分析 (1)根據(jù)△ABC是正三角形,得出∠ADB=∠BDC=60°,再根據(jù)DM=DC,得到DM=CM=CD,最后根據(jù)∠ADB=∠DMC=60°,可判定CM∥AD;
(2)先根據(jù)△ADC≌△BMC,得出BD=3,再根據(jù)△ADE∽△CME,得到DE=$\frac{2}{3}$,ME=$\frac{4}{3}$,且AE=$\frac{1}{3}$AC,最后判定△ABE∽△DCE,得出$\frac{DC}{AB}$=$\frac{EC}{BE}$,即$\frac{2}{AB}$=$\frac{\frac{2}{3}AC}{1+\frac{4}{3}}$,求得AB=$\sqrt{7}$=BC,根據(jù)AE:CE=AD:CD=1:2,可得CE=$\frac{2}{3}$AC,最后根據(jù)△BCE的面積=$\frac{2}{3}$×△ABC的面積,求得S△BCE即可.
解答 解:(1)∵△ABC是正三角形,
∴$\widehat{AB}$=$\widehat{BC}$,
∴∠ADB=∠BDC=60°,
又∵DM=DC,
∴△CDM是等邊三角形,即DM=CM=CD,
∴∠DMC=60°,
∴∠ADB=∠DMC=60°,
∴CM∥AD;
(2)∵∠DAC=∠DBC,∠BMC=∠ADC=120°,而AC=BC,
∴△ADC≌△BMC,
∴BM=AD=1,
∴BD=BM+MD=1+2=3,
由(1)可得,△ADE∽△CME,而AD=1,CM=2,
∴$\frac{AD}{CM}$=$\frac{AE}{CE}$=$\frac{DE}{ME}$=$\frac{1}{2}$,
又∵M(jìn)D=2,
∴DE=$\frac{2}{3}$,ME=$\frac{4}{3}$,
∵$\frac{AE}{CE}$=$\frac{1}{2}$,且點E在線段AC上,
∴AE=$\frac{1}{3}$AC,
∵∠BAC=∠BDC=60°,∠ABD=∠ACD,
∴△ABE∽△DCE,
∴$\frac{DC}{AB}$=$\frac{EC}{BE}$,
∴$\frac{2}{AB}$=$\frac{\frac{2}{3}AC}{1+\frac{4}{3}}$,
又∵AB=AC,
∴AB2=7,即AB=$\sqrt{7}$=BC,
∵AD=1,CM=2,CM=CD,
∴AD:CD=1:2,
又∵∠ADE=∠CDE=60°,
∴BD平分∠ADC,
∴AE:CE=AD:CD=1:2,
∴CE=$\frac{2}{3}$AC,
∴△BCE的面積=$\frac{2}{3}$×△ABC的面積=$\frac{2}{3}$×$\frac{\sqrt{3}}{4}$×($\sqrt{7}$)2=$\frac{7}{6}\sqrt{3}$.
點評 本題主要考查了三角形的外接圓與外心、等邊三角形的性質(zhì)以及角平分線的性質(zhì)的綜合應(yīng)用,解決問題的關(guān)鍵是根據(jù)全等三角形的性質(zhì)以及相似三角形的性質(zhì)進(jìn)行求解.


科目:初中數(shù)學(xué) 來源: 題型:解答題
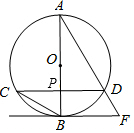 如圖,AB為⊙O的直徑,弦CD⊥AB,垂足為點P,直線BF與AD延長線交于點F,且∠AFB=∠ABC.
如圖,AB為⊙O的直徑,弦CD⊥AB,垂足為點P,直線BF與AD延長線交于點F,且∠AFB=∠ABC.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | msin40° | B. | mcos40° | C. | mtan40° | D. | $\frac{m}{tan40°}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
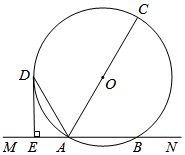 如圖,直線MN交⊙O于A,B兩點,AC是⊙O的直徑,DE與⊙O相切于點D,且DE⊥MN于點E.
如圖,直線MN交⊙O于A,B兩點,AC是⊙O的直徑,DE與⊙O相切于點D,且DE⊥MN于點E.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
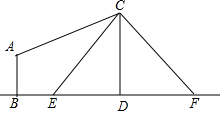 如圖,電線桿CD上的C處引拉線CE,CF固定電線桿,在離電線桿6米的B處安置測角儀(點B,E,D在同一直線上),在A處測得電線桿上C處的仰角為30°,已知測角儀的高AB=1.5米,BE=2.3米,求拉線CE的長,(精確到0.1米)參考數(shù)據(jù)$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73.
如圖,電線桿CD上的C處引拉線CE,CF固定電線桿,在離電線桿6米的B處安置測角儀(點B,E,D在同一直線上),在A處測得電線桿上C處的仰角為30°,已知測角儀的高AB=1.5米,BE=2.3米,求拉線CE的長,(精確到0.1米)參考數(shù)據(jù)$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 定理:等腰三角形的兩個底角相等(簡稱“等邊對等角”).
定理:等腰三角形的兩個底角相等(簡稱“等邊對等角”).查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com