
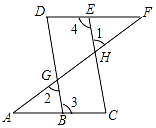
 如圖,點E在直線DF上,點B在直線AC上,若∠1=∠2,∠3=∠4,求證:∠A=∠F
如圖,點E在直線DF上,點B在直線AC上,若∠1=∠2,∠3=∠4,求證:∠A=∠F 分析 先證明BD∥CE,得出同旁內角互補∠3+∠C=180°,再由已知得出∠4+∠C=180°,證出 AC∥DF,即可得出結論.
解答 解:∵∠1=∠2(已知)
∠2=∠DGF (對頂角相等)
∴∠1=∠DGF( 等量代換 )
∴BD∥CE (同位角相等,兩直線平行)
∴∠3+∠C=180° (兩直線平行,同旁內角互補)
又∵∠3=∠4(已知)
∴∠4+∠C=180°
∴AC∥DF∥(同旁內角互補,兩直線平行)
∴∠A=∠F (兩直線平行,內錯角相等);
故答案為:對頂角相等;∠DGF;同位角相等,兩直線平行;兩直線平行,同旁內角互補;AC,DF;兩直線平行,內錯角相等.
點評 本題考查了平行線的判定與性質、對頂角相等的性質;熟練掌握平行線的判定與性質是解決問題的關鍵,注意兩者的區(qū)別.


 課時訓練江蘇人民出版社系列答案
課時訓練江蘇人民出版社系列答案 黃岡經(jīng)典趣味課堂系列答案
黃岡經(jīng)典趣味課堂系列答案 啟東小題作業(yè)本系列答案
啟東小題作業(yè)本系列答案科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
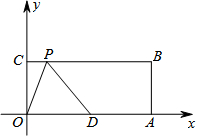 已知,如圖:在平面直角坐標系中,O為坐標原點,OABC是長方形,點A、C的坐標分別為A(20,0),C(0,8),點D是OA的中點,點P在BC邊上運動,△ODP是腰長為10的等腰三角形時,求滿足條件的點P點坐標.
已知,如圖:在平面直角坐標系中,O為坐標原點,OABC是長方形,點A、C的坐標分別為A(20,0),C(0,8),點D是OA的中點,點P在BC邊上運動,△ODP是腰長為10的等腰三角形時,求滿足條件的點P點坐標.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
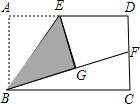 (1)操作發(fā)現(xiàn):如圖,小明在矩形紙片ABCD的邊AD上取中點E,將△ABE沿BE折疊后得到△GBE,且點G在矩形ABCD內部,將BG延長交DC于點F,認為GF=DF,你同意嗎?說明理由.
(1)操作發(fā)現(xiàn):如圖,小明在矩形紙片ABCD的邊AD上取中點E,將△ABE沿BE折疊后得到△GBE,且點G在矩形ABCD內部,將BG延長交DC于點F,認為GF=DF,你同意嗎?說明理由.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
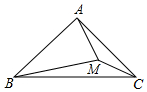 如圖,在△ABC中,∠BAC=90°,AB=AC,M為△ABC內一點,恰好滿足BA=BM,AM=CM,則∠ABM的度數(shù)為30°.
如圖,在△ABC中,∠BAC=90°,AB=AC,M為△ABC內一點,恰好滿足BA=BM,AM=CM,則∠ABM的度數(shù)為30°.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
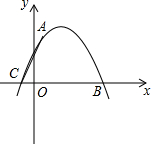 如圖,二次函數(shù)y=ax2+bx+c的圖象經(jīng)過點A(1,4)與B(5,0),C(-1,0).
如圖,二次函數(shù)y=ax2+bx+c的圖象經(jīng)過點A(1,4)與B(5,0),C(-1,0).查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com