
分析 如圖(1)和(2),由等腰三角形的外心在三角形的底邊的高上,根據勾股定理求出OD的長,進一步求出BD的長,根據三角形的面積公式即可求出答案.
解答 解:連接OB交AC于D,連接OC,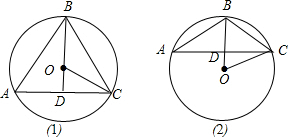
∵圓O是等腰三角形的外接圓,O是外心,
∴BD⊥AC,AD=DC=4,有兩種情況:
(1)如圖(1):OC=5,由勾股定理得:OD=$\sqrt{O{C}^{2}-C{D}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
即:BD=3+5=8,
∴S△ABC=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×8×8=32;
(2)如圖(2):同法可求OD=3,
BD=5-3=2,
∴S△ABC=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×8×2=8;
故答案為:32或8.
點評 本題主要考查了三角形的外接圓和外心,等腰三角形的性質,勾股定理,三角形的面積等知識點,解此題的關鍵是求出高BD的長度.此題用的數學思想是分類討論思想.題目較好.


 名校聯盟快樂課堂系列答案
名校聯盟快樂課堂系列答案 黃岡創優卷系列答案
黃岡創優卷系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
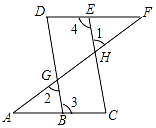 如圖,點E在直線DF上,點B在直線AC上,若∠1=∠2,∠3=∠4,求證:∠A=∠F
如圖,點E在直線DF上,點B在直線AC上,若∠1=∠2,∠3=∠4,求證:∠A=∠F 查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
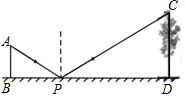 如圖是小王同學設計的測量樹高的示意圖.在點P處放一水平的平面鏡,小王同學站在地面的B處,通過平面鏡剛好能看見大樹CD的頂端C,若小王身高AB=1.6米,BP=3米,PD=15米,則大樹的高度CD是8米.
如圖是小王同學設計的測量樹高的示意圖.在點P處放一水平的平面鏡,小王同學站在地面的B處,通過平面鏡剛好能看見大樹CD的頂端C,若小王身高AB=1.6米,BP=3米,PD=15米,則大樹的高度CD是8米.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
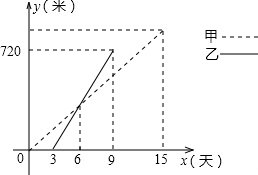 如皋某鄉鎮決定對A、B兩村之間的公路進行改造,并有甲工程隊從A村向B村方向修筑,乙工程隊從B村向A村方向修筑.已知甲工程隊先施工3天,乙工程隊再開始施工.乙工程隊施工幾天后因另有任務提前離開,余下的任務由甲工程隊單獨完成,直到公路修通.下圖是甲乙兩個工程隊修公路的長度y(米)與施工時間x(天)之間的函數圖象,請根據圖象所提供的信息解答下列問題:
如皋某鄉鎮決定對A、B兩村之間的公路進行改造,并有甲工程隊從A村向B村方向修筑,乙工程隊從B村向A村方向修筑.已知甲工程隊先施工3天,乙工程隊再開始施工.乙工程隊施工幾天后因另有任務提前離開,余下的任務由甲工程隊單獨完成,直到公路修通.下圖是甲乙兩個工程隊修公路的長度y(米)與施工時間x(天)之間的函數圖象,請根據圖象所提供的信息解答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
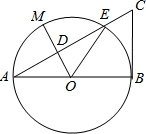 如圖,以線段AB為直徑的⊙O交線段AC于點E,點M是$\widehat{AE}$ 的中點,OM交AC于點D,BC=2$\sqrt{3}$,∠BOE=60°,∠C=60°.
如圖,以線段AB為直徑的⊙O交線段AC于點E,點M是$\widehat{AE}$ 的中點,OM交AC于點D,BC=2$\sqrt{3}$,∠BOE=60°,∠C=60°.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com