
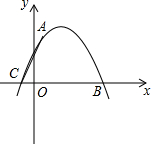
 如圖,二次函數y=ax2+bx+c的圖象經過點A(1,4)與B(5,0),C(-1,0).
如圖,二次函數y=ax2+bx+c的圖象經過點A(1,4)與B(5,0),C(-1,0).分析 (1)把A、B、C的坐標代入二次函數解析式求出a、b、c的值即可;
(2)如圖,過A作x軸的垂直,垂足為E(1,0),連接ED、DB,過D作DF⊥AE,DG⊥x軸,垂足分別為F,G,分別表示出三角形ACE,三角形ADE,以及三角形BDE的面積,之和即為S,確定出S關于x的函數解析式,并求出x的范圍,利用二次函數性質即可確定出S的最大值,以及此時x的值;
(3)由于AC確定,得到點E與點A的縱坐標之間的關系,然后代入拋物線的解析式,就可得到滿足條件的所有點E的坐標.
解答 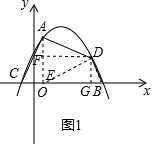 解:(1)把點A(1,4)與B(5,0),C(-1,0)代入y=ax2+bx+c得:$\left\{\begin{array}{l}{a+b+c=4}\\{25a+5b+c=0}\\{a-b+c=0}\end{array}\right.$,
解:(1)把點A(1,4)與B(5,0),C(-1,0)代入y=ax2+bx+c得:$\left\{\begin{array}{l}{a+b+c=4}\\{25a+5b+c=0}\\{a-b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=2}\\{c=\frac{5}{2}}\end{array}\right.$,
∴該二次函數的解析式為:y=-$\frac{1}{2}$x2+2x+$\frac{5}{2}$;
(2)如圖1,過A作x軸的垂直,垂足為E(1,0),連接ED、DB,過D作DF⊥AE,DG⊥x軸,垂足分別為F,G,
S△ACE=$\frac{1}{2}$CE•AE=$\frac{1}{2}$×2×4=4;
S△ADE=$\frac{1}{2}$AE•DF=$\frac{1}{2}$×4×(x-1)=2x-2;
S△BDE=$\frac{1}{2}$BE•DG=$\frac{1}{2}$×4×(-$\frac{1}{2}$x2+2x+$\frac{5}{2}$)=-x2+4x+5,
則S=S△ACE+S△ADE+S△BDE=4+2x-2-x2+4x+5=-x2+6x+7,
∴S關于x的函數表達式為S=-x2+6x+7(1<x<5),
∵S=-x2+6x+7=-(x-3)2+16,
∴當x=3時,四邊形OACB的面積S有最大值,最大值為16;
(3)∵AC為平行四邊形的一邊,則AC∥EF,AE∥CF,A,E到x軸的距離相等,
∴|yE|=|yA|=4,
∴yE=±4.
當yE=4時,解方程-$\frac{1}{2}$x2+2x+$\frac{5}{2}$=4得,
x1=1,x2=3,
∴點E的坐標為(3,4);
當yE=-4時,解方程-$\frac{1}{2}$x2+2x+$\frac{5}{2}$=-4得,
x1=2-$\sqrt{17}$,x2=2+$\sqrt{17}$,
∴點E的坐標為(2-$\sqrt{17}$,-4),(2+$\sqrt{17}$,-4).
點評 本題屬于二次函數綜合題,主要考查了運用待定系數法求出直線及拋物線的解析式、拋物線上點的坐標特征、解一元二次方程、平行四邊形的性質、拋物線的性質等知識的綜合應用,運用割補法及配方法是解決問題的關鍵,解題時注意運用分類討論的思想.


 輕松暑假總復習系列答案
輕松暑假總復習系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
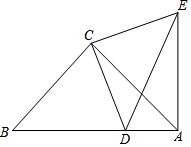 如圖,△ABC和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D為AB上一點.
如圖,△ABC和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D為AB上一點.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
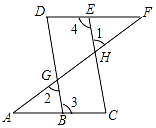 如圖,點E在直線DF上,點B在直線AC上,若∠1=∠2,∠3=∠4,求證:∠A=∠F
如圖,點E在直線DF上,點B在直線AC上,若∠1=∠2,∠3=∠4,求證:∠A=∠F 查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com