
 如圖,?ABCD中,BD⊥AD,AD=24,BD=10,求CD及AC的長.
如圖,?ABCD中,BD⊥AD,AD=24,BD=10,求CD及AC的長. 分析 根據勾股定理,可得AB的長,根據平行四邊的性質,可得CD的長;根據平行四邊形的性質,可得OD的長,根據勾股定理,可得AO的長,再根據平行四邊形的性質,可得AC的長.
解答 解:由BD⊥AD,得∠AOD=90°.
由勾股定理,得
AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{2{4}^{2}+1{0}^{2}}$=$\sqrt{576}$,
由平行四邊形的對邊相等,得
CD=AB=$\sqrt{676}$.
由平行四邊形的對角線互相平分,得
DO=BO=5,AO=CO.
由勾股定理,得
AO=$\sqrt{A{D}^{2}+D{O}^{2}}$=$\sqrt{2{4}^{2}+{5}^{2}}$=$\sqrt{601}$,
AC=2AO=2$\sqrt{601}$.
點評 本題考查了平行四邊形的性質,熟記平行四邊形的性質是解題關鍵,平行四邊形的對邊相等,平行四邊形的對角線互相平分.


科目:初中數學 來源: 題型:解答題
 如圖所示,△ABC中,AB=AC,E是AB上一點,F在AC的延長線上,BE=CF,連接EF交BC于D,過E作EG∥AF交BC于G.
如圖所示,△ABC中,AB=AC,E是AB上一點,F在AC的延長線上,BE=CF,連接EF交BC于D,過E作EG∥AF交BC于G.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
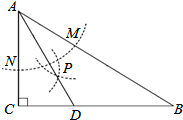 如圖,在△ABC中,∠C=90°,∠B=30°,以A為圓心,任意長為半徑畫弧分別交AB、AC于點M和N,再分別以M、N為圓心,大于$\frac{1}{2}$MN的長為半徑畫弧,兩弧交于點P,連結AP并延長交BC于點D,則下列說法中正確的個數是( )
如圖,在△ABC中,∠C=90°,∠B=30°,以A為圓心,任意長為半徑畫弧分別交AB、AC于點M和N,再分別以M、N為圓心,大于$\frac{1}{2}$MN的長為半徑畫弧,兩弧交于點P,連結AP并延長交BC于點D,則下列說法中正確的個數是( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系中,直線y=mx+n和雙曲線y=$\frac{k}{x}$交于A、B,點B的坐標是(2,-3),AC⊥y軸于點C,AC=$\frac{3}{2}$,求雙曲線和直線所對應的函數關系式.
如圖,在平面直角坐標系中,直線y=mx+n和雙曲線y=$\frac{k}{x}$交于A、B,點B的坐標是(2,-3),AC⊥y軸于點C,AC=$\frac{3}{2}$,求雙曲線和直線所對應的函數關系式.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,把矩形紙片OABC放入平面直角坐標系中,使OA、OC分別落在x軸,y軸上,連結OB,將紙片OABC沿OB對折,使點A落在點E的位置,若OB=$\sqrt{5}$,tan∠BOC=$\frac{1}{2}$,則點E的坐標為( )
如圖,把矩形紙片OABC放入平面直角坐標系中,使OA、OC分別落在x軸,y軸上,連結OB,將紙片OABC沿OB對折,使點A落在點E的位置,若OB=$\sqrt{5}$,tan∠BOC=$\frac{1}{2}$,則點E的坐標為( )| A. | (-$\frac{4}{5},\frac{3}{5}$) | B. | (-$\frac{3}{5},\frac{4}{5}$) | C. | (-1,1) | D. | (-1,2) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 為迎接省衛生文明城市建設,某校把一塊形狀為直角三角形的廢地開辟為植物園.如圖所示,∠ACB=90°,AC=80m,BC=60m.若線段CD是一條水渠,且CD⊥AB,已知水渠的造價為100元/m,求水渠CD的長及其造價.
為迎接省衛生文明城市建設,某校把一塊形狀為直角三角形的廢地開辟為植物園.如圖所示,∠ACB=90°,AC=80m,BC=60m.若線段CD是一條水渠,且CD⊥AB,已知水渠的造價為100元/m,求水渠CD的長及其造價.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com