Question

9．如圖，把矩形紙片OABC放入平面直角坐標系中，使OA、OC分別落在x軸，y軸上，連結OB，將紙片OABC沿OB對折，使點A落在點E的位置，若OB=$\sqrt{5}$，tan∠BOC=$\frac{1}{2}$，則點E的坐標為（　　）

• A． （-$\frac{4}{5}，\frac{3}{5}$）
• B． （-$\frac{3}{5}，\frac{4}{5}$）
• C． （-1，1）
• D． （-1，2）

Answer 1

分析 過點E作ED⊥x軸與點D，根據題意首先求出AB、BC的長度；借助面積公式求出ED、OD的長度，即可解決問題．

解答 解：如圖，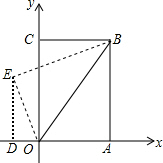

過點E作ED⊥x軸與點D；
設ED=x，OD=y；
∵四邊形ABCO為矩形，
∴∠OAB=∠OCB=90°；四邊形ABED為梯形；
設AB=OC=a，BC=AO=b；
∵OB=$\sqrt{5}$，tan∠BOC=$\frac{1}{2}$，
∴$\left\{\begin{array}{l}{{a}^{2}+{b}^{2}=5}\\{\frac{b}{a}=\frac{1}{2}}\end{array}\right.$，
解得：a=2，b=1；
由題意得：EO=AO=1；△ABO≌△EBO；
由勾股定理得：x²+y²=1①，
由面積公式得：$\frac{1}{2}$xy+2×$\frac{1}{2}$×2×1=$\frac{1}{2}$（x+2）（y+1）②；
聯立①②并解得：x=$\frac{4}{5}$，y=$\frac{3}{5}$，
則點E的坐標為（-$\frac{3}{5}$，$\frac{4}{5}$）．
故選：B．

點評 此題考查翻折變換，坐標與圖形的性質；綜合利用矩形的性質、三角函數的定義、勾股定理等幾何知識點解決問題．