
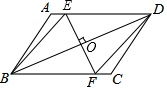
 如圖,在平行四邊形ABCD中,點O是對角線BD的中點,過O點作EF⊥BD,交AD于E,交BC于F,那么,四邊形EBFD是菱形嗎?為什么?
如圖,在平行四邊形ABCD中,點O是對角線BD的中點,過O點作EF⊥BD,交AD于E,交BC于F,那么,四邊形EBFD是菱形嗎?為什么? 分析 首先證明△DOE≌△BOF可得BF=DE,再有平行四邊形的性質可得AD∥BC,進而可得四邊形EDFB是平行四邊形,再由條件EF⊥BD可得四邊形EBFD是菱形.
解答 解:四邊形EBFD是菱形,
∵四邊形ABCD是平行四邊形,
∴AD∥BC,
∴∠DEO=∠OFB,
∵點O是對角線BD的中點,
∴BO=DO,
在△EDO和△FBO中$\left\{\begin{array}{l}{∠DEO=∠OFB}\\{∠EOD=∠FOB}\\{BO=DO}\end{array}\right.$,
∴△DOE≌△BOF(AAS),
∴BF=DE,
∴四邊形EDFB是平行四邊形,
∵EF⊥BD,
∴四邊形EBFD是菱形.
點評 此題主要考查了菱形的判定,關鍵是掌握對角線互相垂直的平行四邊形是菱形.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
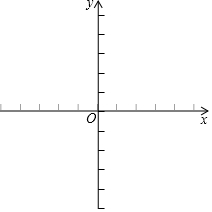 已知平行四邊形的三個頂點的坐標分別為(1,1)(5,1)(2,4).請你在下面的坐標系中畫出這三個點,根據這三個點的位置畫出一個平行四邊形,并寫出第四個點的坐標.
已知平行四邊形的三個頂點的坐標分別為(1,1)(5,1)(2,4).請你在下面的坐標系中畫出這三個點,根據這三個點的位置畫出一個平行四邊形,并寫出第四個點的坐標.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com