

分析 (1)①由條件可得BN=BM,再用t表示出線段的長度,代入可求得t的值;
②設運動時間為t秒,分別表示CM和BN.分兩種情況,運用特殊三角形的性質求解:I.∠NMB=90°;Ⅱ.∠BNM=90°;
(2)①如圖1中,當點M在BC上,點N在AB上時,如果BM=CM,BN=CD,因為∠B=∠C=60°,則△DCM≌△NBM,求出點M的運動時間即可解決問題.
②如圖2中,當點M在線段AB上,點N在線段AC上時,如果點N與點D重合,BM=CD時,則△DCM≌△MBN,求出點M的運動時間即可解決問題.
解答 解:(1)①∵MN∥AC且△ABC為等邊三角形,
∴BN=BM,
∵BN=2t,BM=10-2t,
∴2t=10-2t,
解得t=2.5,
故運動時間t為2.5時,MN∥AC;
②設運動時間為t秒,△BMN是直角三角形有兩種情況:
Ⅰ.當∠NMB=90°時,
∵∠B=60°,
∴∠BNM=90°-∠B=90°-60°=30°.
∴BN=2BM,
∴2t=2×(10-2t)
∴t=$\frac{10}{3}$(秒);
Ⅱ.當∠BNM=90°時,
∵∠B=60°,
∴∠BMN=90°-∠B=90°-60°=30°.
∴BM=2BN,
∴10-2t=2×2t
∴t=$\frac{5}{3}$(秒);
∴當t=$\frac{10}{3}$秒或t=$\frac{5}{3}$秒時,△BMN是直角三角形;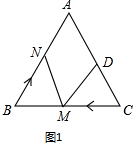
(2)①如圖1中,當點M在BC上,點N在AB上時,如果BM=CM,BN=CD,因為∠B=∠C=60°,
∴△DCM≌△NBM,
∴BM=CM=5,BN=CD=4,
∴點M的運動時間t=$\frac{5}{2}$,
∴點N的運動速度=$\frac{4}{\frac{5}{2}}$=$\frac{8}{5}$cm/秒.
②如圖2中,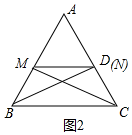 當點M在線段AB上,點N在線段AC上時,如果點N與點D重合,BM=CD時,
當點M在線段AB上,點N在線段AC上時,如果點N與點D重合,BM=CD時,
∴△DCM≌△MBN,
∴BM=CD=4,AN=6,
∴點M的運動時間t=$\frac{14}{2}$=7秒,
∴點N的運動速度=$\frac{16}{7}$cm/秒.
綜上所述,點N的速度為$\frac{8}{5}$cm/秒或$\frac{16}{7}$cm/秒時,△BMN和△CDM的構成全等
點評 本題考查三角形綜合題、全等三角形的判定和性質、直角三角形的性質、路程、速度、時間的關系等知識,解題的關鍵是靈活運用所學知識解決問題,學會用分類討論的思想思考問題,屬于中考壓軸題.


科目:初中數學 來源: 題型:選擇題
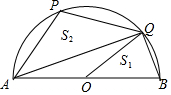 如圖,在半圓O中,AB為直徑,點P是圓上一點,連結AP,過O作OQ∥AP與半圓交于點Q,設△OQB的面積為S1,△APQ的面積為S2,若$\frac{{S}_{1}}{{S}_{2}}$=$\frac{5}{6}$,則tan∠PQA的值為( )
如圖,在半圓O中,AB為直徑,點P是圓上一點,連結AP,過O作OQ∥AP與半圓交于點Q,設△OQB的面積為S1,△APQ的面積為S2,若$\frac{{S}_{1}}{{S}_{2}}$=$\frac{5}{6}$,則tan∠PQA的值為( )| A. | $\frac{5}{6}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
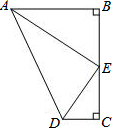 如圖,點E是BC的中點,AB⊥BC,DC⊥BC,AE平分∠BAD,下列結論:①∠AED=90°;②∠ADE=∠AEB;③S梯形ABCD=AD•CE;④AD=2AE,四個結論中成立的是( )
如圖,點E是BC的中點,AB⊥BC,DC⊥BC,AE平分∠BAD,下列結論:①∠AED=90°;②∠ADE=∠AEB;③S梯形ABCD=AD•CE;④AD=2AE,四個結論中成立的是( )| A. | ①②④ | B. | ①②③ | C. | ②③④ | D. | ①③④ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
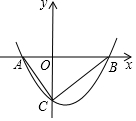 平面直角坐標系中,將拋物線y=ax2經平移后與x軸交于點A、B,與y軸交于點C,若$\frac{{{S_{△AOC}}}}{{{S_{△BOC}}}}=\frac{{\sqrt{5}-1}}{2}$,則稱平移后的拋物線所在的位置為拋物線y=ax2在該平面直角坐標系中的一個“黃金位”.如圖所示的拋物線為拋物線y=ax2的一個“黃金位”,且AB=2,將圖中的拋物線向右平移$\frac{5+\sqrt{5}}{2}$個單位長度又可得到拋物線y=ax2的另一個“黃金位”.
平面直角坐標系中,將拋物線y=ax2經平移后與x軸交于點A、B,與y軸交于點C,若$\frac{{{S_{△AOC}}}}{{{S_{△BOC}}}}=\frac{{\sqrt{5}-1}}{2}$,則稱平移后的拋物線所在的位置為拋物線y=ax2在該平面直角坐標系中的一個“黃金位”.如圖所示的拋物線為拋物線y=ax2的一個“黃金位”,且AB=2,將圖中的拋物線向右平移$\frac{5+\sqrt{5}}{2}$個單位長度又可得到拋物線y=ax2的另一個“黃金位”.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com