Question

6．圓內一弦與直徑相交成30°，且分直徑為2cm和10cm兩部分，則該弦長為8$\sqrt{2}$cm．

Answer 1

分析 根據題目中的條件，畫出相應的圖形，再根據垂徑定理和勾股定理即可求得弦長，本題得以解決．

解答 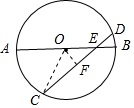解：如右圖所示，AB為圓的直徑，與弦CD相交的∠AEC=30°，AE=10cm，BE=2cm，
∴AB=12cm，
∴OE=4cm，
作OF⊥CD于點F，
∵OE=4cm，∠AEC=30°，
∴OF=2cm，
連接OC，
∴CF=$\sqrt{{6}^{2}-{2}^{2}}=4\sqrt{2}$，
∴CD=8$\sqrt{2}$cm，
故答案為：8$\sqrt{2}$．

點評 本題考查垂徑定理、30°角所對的直角邊與斜邊的關系、勾股定理，解答本題的關鍵是明確題意，畫出相應的圖形，利用數形結合的思想解答．