
分析 (1)根據ab>0,確定a、b同號,根據$\sqrt{(a-b)^{2}}$=b-a確定b≥a,則a=4,b=7,代入求值即可;
(2)先確定x的值,當(x-1)2最小時,代數式100-(x-1)2有最大值,再化簡代入求值.
解答 解:(1)|a|=4,|b|=7,
∴a=±4,b=±7,
∵ab>0,
∴a、b同號,
由$\sqrt{(a-b)^{2}}$=b-a得:b≥a,
∴a=4,b=7,
∴a-2b+1=4-2×7+1=-9;
(2)當x=1時,100-(x-1)2有最大值,
則-3(x-5)-(2x+7),
=-3x+15-2x-7,
=-5x+8,
當x=1時,原式=-5×1+8=3.
點評 此題考查了絕對值的意義、二次根式的性質、偶次方的非負性及整式的加減-化簡求值問題,熟練掌握運算法則是解本題的關鍵.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:初中數學 來源: 題型:解答題
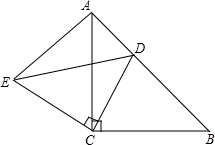 如圖,△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,且點D在AB邊上,連接AE,
如圖,△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,且點D在AB邊上,連接AE,查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (x-$\frac{1}{2}$)2=0 | B. | (x-$\frac{1}{2}$)2=$\frac{1}{2}$ | C. | (x-1)2=$\frac{1}{2}$ | D. | (x-1)2=0 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 (1)計算:|$\sqrt{3}$-2|+20150-($\frac{1}{3}$)+3tan30°;
(1)計算:|$\sqrt{3}$-2|+20150-($\frac{1}{3}$)+3tan30°;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com