Question

7．如圖，⊙O是△ABC的外接圓，∠A=30°，AB是⊙O的直徑，過點C作⊙O的切線，交AB延長線于D，CD=6$\sqrt{3}$cm．

（1）求證：AC=CD；
（2）求AB的長；
（3）若動點M以3cm/s的速度從A出發沿AB方向運動，同時點N以1.5cm/s的速度從B點出發沿BC方向運動，設運動的時間為t（0≤t≤2），連接△BMN，當t為何值時△BMN為直角三角形？

Answer 1

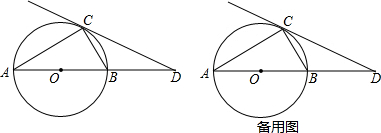
分析 （1）連接OC，根據等腰三角形的性質得到∠OCA=∠A=30°，根據切線的性質得到∠OCD=90°，計算出∠D=30°，根據等腰三角形的判定定理證明即可；
（2）根據正切的概念求出OC的長，計算出AB的長；
（3）分∠MNB=90°和∠NMB=90°兩種情況，根據相似三角形的判定定理和性質定理列出比例式，計算即可．

解答 （1）證明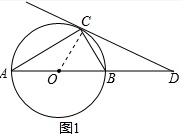：如圖1，連接OC，
∵OA=OC，
∴∠OCA=∠A=30°，
∴∠COD=60°，
∵CD為⊙O的切線，
∴∠OCD=90°，
∴∠D=30°，
∴∠A=∠D，
∴AC=CD；
（2）解：∵∠OCD=90°，∠D=30°，CD=6$\sqrt{3}$cm，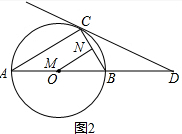
∴OC=CD•tan∠D=6，
∴AB=12；
（3）解：如圖2，∠MNB=90°時，
由題意得，AM=3t，BN=1.5t，
∵AB是⊙O的直徑，
∴∠ACB=90°，又∠MNB=90°，
∴MN∥AC，
∴$\frac{BM}{BA}$=$\frac{BN}{BC}$，即$\frac{12-3t}{12}$=$\frac{1.5t}{6}$，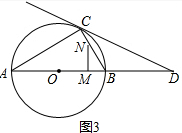
解得t=2s；
如圖3，∠NMB=90°時，
△BNM∽△BAC，
∴$\frac{BM}{BC}$=$\frac{BN}{BA}$，即$\frac{12-3t}{6}$=$\frac{1.5t}{12}$，
解得t=3.2（舍去）．
∴當t=2s時，△BMN為直角三角形．

點評 本題考查的是切線的性質定理、直角三角形的性質、勾股定理的應用，相似三角形的判定和性質定理，正確作出輔助線、靈活運用相關定理是解題的關鍵，注意分情況討論思想的正確應用．