
 如圖,二次函數(shù)y=ax2+bx+c的最大值為$\frac{13}{6}$,其圖象經(jīng)過點A(0,-2)、B(5,-2),點C在x軸上,∠ACB=90°,且CA<CB,將△ABC饒點A逆時針旋轉(zhuǎn),使點C的對應(yīng)點C′落在x軸上.
如圖,二次函數(shù)y=ax2+bx+c的最大值為$\frac{13}{6}$,其圖象經(jīng)過點A(0,-2)、B(5,-2),點C在x軸上,∠ACB=90°,且CA<CB,將△ABC饒點A逆時針旋轉(zhuǎn),使點C的對應(yīng)點C′落在x軸上.分析 (1)利用頂點坐標縱坐標公式:$\frac{4ac-{b}^{2}}{4a}$代入得一方程,再把A(0,-2)、B(5,-2)代入拋物線中列方程組可求解;
(2)作輔助線,構(gòu)建全等三角形,證明△BCD≌△B′C′E,則B′E=BD=2,C′E=CD,再利用相似得:AF的長為1和4,因為AC<CB,則AF=4不符合題意,由旋轉(zhuǎn)的性質(zhì)得△ACC′是等腰三角形,由三線合一得:OC=OC′=1,從而求得OE的長,得出點B′的坐標,并計算當x=3時,對應(yīng)的y值,等于2,則在拋物線上,不等于2,則不在拋物線上;
(3)先根據(jù)勾股定理求B′P=$\frac{5}{2}$,根據(jù)S△B′PQ=S△OAP,可求出△B′PQ以B′P為底邊時的高為$\frac{6}{5}$,則作AB′的平行線且距離為$\frac{6}{5}$,與拋物線交于Q1、Q2,根據(jù)兩解析式列方程組可得結(jié)論.
解答 解:(1)由題意得:$\left\{\begin{array}{l}{\frac{4ac-{b}^{2}}{4a}=\frac{13}{6}}\\{c=-2}\\{25a+5b+c=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{2}{3}}\\{b=\frac{10}{3}}\\{c=-2}\end{array}\right.$,
∴二次函數(shù)的解析式為:y=-$\frac{2}{3}{x}^{2}+\frac{10}{3}x-2$;
(2)過B作BD⊥x軸于D,過B′作B′E⊥x軸于E,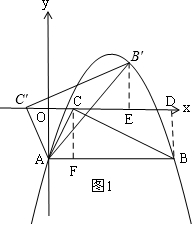
則∠C′EB′=∠BDC=90°,
由旋轉(zhuǎn)得:BC=B′C′,AC=AC′,
∴∠AC′C=∠ACC′,
∵∠ACB=90°,
∴∠BCD+∠ACC′=90°,
∵∠AC′C+∠B′C′C=90°,
∴∠BCD=∠B′C′C,
∴△BCD≌△B′C′E,
∴B′E=BD=2,C′E=CD,
過C作CF⊥AB于F,
設(shè)AF=x,則BF=5-x,
∵∠CAB+∠ACF=90°,∠ACF+∠FCB=90°,
∴∠CAB=∠FCB,
∵∠AFC=∠BFC=90°,
∴△AFC∽△CFB,
∴$\frac{AF}{CF}=\frac{CF}{FB}$,
∴CF2=AF•FB,
∵B(5,-2),
∴CF=2,
∴22=x(5-x),
x2-5x+4=0,
(x-1)(x-4)=0,
x=1或4,
∵AC<CB,
∴x=4不符合題意,舍,
∴AF=OC=1,
∴CD=BF=CE=5-1=4,
∵AC=AC′,AO⊥CC′,
∴OC=OC′=1,
∴OE=C′E-OC′=4-1=3,
∴B′(3,2),
當x=3時,y=-$\frac{2}{3}$×9+$\frac{10}{3}$×3-2=2,
∴B′落在二次函數(shù)的圖象上;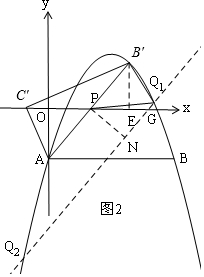
(3)存在,設(shè)AB′的解析式為:y=kx+b,
把A(0,-2)、B′(3,2)代入得:$\left\{\begin{array}{l}{b=-2}\\{3k+b=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=-2}\end{array}\right.$,
∴AB′的解析式為:y=$\frac{4}{3}$x-2,
當y=0時,$\frac{4}{3}$x-2=0,
x=$\frac{3}{2}$,
∴P($\frac{3}{2}$,0),
∴OP=$\frac{3}{2}$,
設(shè)拋物線上任意一點為Q1,過Q1作AB′的平行線,交拋物線于Q2,交x軸于G,過P作PN⊥AB′于N,則PN⊥Q1Q2,
在Rt△B′PE中,B′E=2,PE=3-$\frac{3}{2}$=$\frac{3}{2}$,
由勾股定理得:B′P=$\sqrt{{2}^{2}+(\frac{3}{2})^{2}}$=$\frac{5}{2}$,
∵S△AOP=${S}_{△B′P{Q}_{1}}$,
∴$\frac{1}{2}$×$\frac{3}{2}$×2=$\frac{1}{2}$×B′P•PN,
3=$\frac{5}{2}$PN,
PN=$\frac{6}{5}$,
∵∠B′PG+∠GPN=90°,
∠GPN+∠PGN=90°,
∴∠B′PG=∠PGN,
∵∠PEB′=∠PNG=90°,
∴△PNG∽△B′EP,
∴$\frac{PG}{PB′}=\frac{PN}{B′E}$,
∴$\frac{PG}{\frac{5}{2}}$=$\frac{\frac{6}{5}}{2}$,
∴PG=$\frac{3}{2}$,
∴OG=OP+PG=$\frac{3}{2}$+$\frac{3}{2}$=3,
∴G(3,0),
設(shè)GQ1的解析式為:y=$\frac{4}{3}$x+b,
把G(3,0)代入得:$\frac{4}{3}$×3+b=0,
b=-4,
∴GQ1的解析式為:y=$\frac{4}{3}$x-4,
則$\left\{\begin{array}{l}{y=\frac{4}{3}x-4}\\{y=-\frac{2}{3}{x}^{2}+\frac{10}{3}x-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=\frac{3+\sqrt{21}}{2}}\\{{y}_{1}=\frac{2\sqrt{21}-6}{3}}\end{array}\right.$ $\left\{\begin{array}{l}{{x}_{2}=\frac{3-\sqrt{21}}{2}}\\{{y}_{2}=\frac{-2\sqrt{21}-6}{3}}\end{array}\right.$,
綜上所述,點Q的坐標是:Q1($\frac{3+\sqrt{21}}{2}$,$\frac{2\sqrt{21}-6}{3}$),Q2($\frac{3-\sqrt{21}}{2}$,$\frac{-2\sqrt{21}-6}{3}$).
點評 本題考查了待定系數(shù)法求二次函數(shù)和一次函數(shù)的解析式,利用了方程組的解求兩函數(shù)的交點坐標;并利用相似和全等的性質(zhì)和判定證明邊的長,寫出對應(yīng)點的坐標.


 智趣寒假作業(yè)云南科技出版社系列答案
智趣寒假作業(yè)云南科技出版社系列答案科目:初中數(shù)學(xué) 來源: 題型:填空題
 如圖,將矩形ABCD沿CE向上折疊,使點B落在AD邊上的點F處.若AE=3,BE=5,則長AD與寬AB的比值是5:4.
如圖,將矩形ABCD沿CE向上折疊,使點B落在AD邊上的點F處.若AE=3,BE=5,則長AD與寬AB的比值是5:4.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖是某座橋的設(shè)計圖,設(shè)計數(shù)據(jù)如圖所示,橋拱是圓弧形,則橋拱的半徑為( )
如圖是某座橋的設(shè)計圖,設(shè)計數(shù)據(jù)如圖所示,橋拱是圓弧形,則橋拱的半徑為( )| A. | 13m | B. | 15m | C. | 20 m | D. | 26m |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖,已知AB是⊙O的直徑,AD切⊙O于點A,點C是$\widehat{EB}$的中點,則下列結(jié)論:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正確的有( )
如圖,已知AB是⊙O的直徑,AD切⊙O于點A,點C是$\widehat{EB}$的中點,則下列結(jié)論:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正確的有( )| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | α=30° | B. | α=45° | C. | 30°<α<45° | D. | 45°<α<60° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
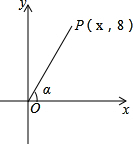 如圖,在平面直角坐標系中,點P在第一象限內(nèi).其坐標是(x,8),且OP與x軸的正半軸的夾角a的正切值是$\frac{4}{3}$.求:
如圖,在平面直角坐標系中,點P在第一象限內(nèi).其坐標是(x,8),且OP與x軸的正半軸的夾角a的正切值是$\frac{4}{3}$.求:查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 已知:如圖,在△ABC中,AB=AC,點D是BC延長線上一點,點E是邊AC上一點,如果∠EBC=∠D,BC=4,cos∠ABC=$\frac{1}{3}$.
已知:如圖,在△ABC中,AB=AC,點D是BC延長線上一點,點E是邊AC上一點,如果∠EBC=∠D,BC=4,cos∠ABC=$\frac{1}{3}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖,△ABC中,∠A=90°,∠C=75°,AC=6,DE垂直平分BC,則BE的值為( )
如圖,△ABC中,∠A=90°,∠C=75°,AC=6,DE垂直平分BC,則BE的值為( )| A. | 12 | B. | 6$\sqrt{3}$ | C. | 8 | D. | 9 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com