
 如圖,已知AB是⊙O的直徑,AD切⊙O于點A,點C是$\widehat{EB}$的中點,則下列結論:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正確的有( )
如圖,已知AB是⊙O的直徑,AD切⊙O于點A,點C是$\widehat{EB}$的中點,則下列結論:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正確的有( )| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
分析 由C為弧EB中點,利用垂徑定理的逆定理得到OC垂直于BE,根據等弧對等弦得到BC=EC,再由AB為直角,利用圓周角定理得到AE垂直于BE,進而得到一對直角相等,利用同位角相等兩直線平行得到OC與AE平行,由AD為圓的切線,利用切線的性質得到AB與DA垂直,利用同角的余角相等得到∠DAE=∠ABE,根據E不一定為弧AC中點,可得出AC與OE不一定垂直,即可確定出結論成立的序號.
解答 解:∵C為$\widehat{EB}$的中點,即$\widehat{BC}=\widehat{CE}$,
∴OC⊥BE,BC=EC,選項②正確;
∴∠BFO=90°,
∵AB為圓O的直徑,
∴AE⊥BE,即∠BEA=90°,
∴∠BFO=∠BEA,
∴OC∥AE,選項①正確;
∵AD為圓的切線,
∴∠DAB=90°,即∠DAE+∠EAB=90°,
∵∠EAB+∠ABE=90°,
∴∠DAE=∠ABE,選項③正確;
點E不一定為$\widehat{AC}$中點,故E不一定是$\widehat{AC}$中點,選項④錯誤,
則結論成立的是①②③,
故選C
點評 此題考查了切線的性質,圓周角定理,平行線的判定,以及垂徑定理,熟練掌握性質及定理是解本題的關鍵.


 新課標快樂提優暑假作業陜西旅游出版社系列答案
新課標快樂提優暑假作業陜西旅游出版社系列答案 暑假銜接培優教材浙江工商大學出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案 欣語文化快樂暑假沈陽出版社系列答案
欣語文化快樂暑假沈陽出版社系列答案科目:初中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
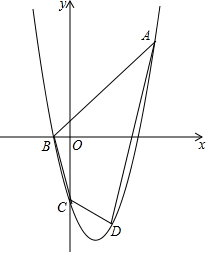 如圖,拋物線y=ax2+bx-4(a≠0)經過點A(5,6),與x軸的負半軸交于點B,與y軸交于點C,且OC=4OB.
如圖,拋物線y=ax2+bx-4(a≠0)經過點A(5,6),與x軸的負半軸交于點B,與y軸交于點C,且OC=4OB.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,在Rt△ABC中,∠C=90°,∠B=60°,將△ABC繞點A逆時針旋轉60°,點B、C分別落在點B'、C'處,聯結BC'與AC邊交于點D,那么$\frac{BD}{DC'}$=$\frac{2}{3}$.
如圖,在Rt△ABC中,∠C=90°,∠B=60°,將△ABC繞點A逆時針旋轉60°,點B、C分別落在點B'、C'處,聯結BC'與AC邊交于點D,那么$\frac{BD}{DC'}$=$\frac{2}{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,二次函數y=ax2+bx+c的最大值為$\frac{13}{6}$,其圖象經過點A(0,-2)、B(5,-2),點C在x軸上,∠ACB=90°,且CA<CB,將△ABC饒點A逆時針旋轉,使點C的對應點C′落在x軸上.
如圖,二次函數y=ax2+bx+c的最大值為$\frac{13}{6}$,其圖象經過點A(0,-2)、B(5,-2),點C在x軸上,∠ACB=90°,且CA<CB,將△ABC饒點A逆時針旋轉,使點C的對應點C′落在x軸上.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
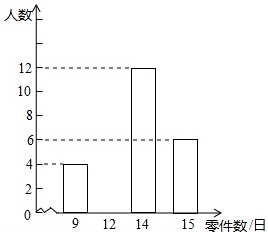 某車間有120名工人,為了了解這些工人日加工零件數的情況,隨機抽出其中的30名工人調查,整理調查結果,繪制出不完整的條形統計圖(如圖).根據圖中的信息,解答下列問題:
某車間有120名工人,為了了解這些工人日加工零件數的情況,隨機抽出其中的30名工人調查,整理調查結果,繪制出不完整的條形統計圖(如圖).根據圖中的信息,解答下列問題:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com