
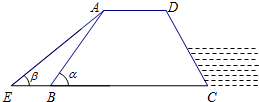
 如圖,防洪大堤的橫斷面是梯形ABCD,其中AD∥BC,坡角α=60°,汛期來臨前對其進行了加固,改造后的坡長為AE,背水面坡角β=45°.若原坡長AB=16m,求改造后的坡長AE(結果保留根號).
如圖,防洪大堤的橫斷面是梯形ABCD,其中AD∥BC,坡角α=60°,汛期來臨前對其進行了加固,改造后的坡長為AE,背水面坡角β=45°.若原坡長AB=16m,求改造后的坡長AE(結果保留根號). 分析 過A作AH⊥BC于H,在Rt△ABH中求出AH的長度,然后在Rt△AEH中求出AE的長度.
解答 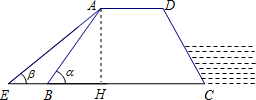 解:過A作AH⊥BC于H.
解:過A作AH⊥BC于H.
在Rt△ABH中,
∵α=60°,AB=16m,
∴AH=AB•sinα=16×$\frac{\sqrt{3}}{2}$=8$\sqrt{3}$,
在Rt△AEH中,
∵β=45°,
∴AE=$\frac{AH}{sin45°}$=$\frac{8\sqrt{3}}{\frac{\sqrt{2}}{2}}$=8$\sqrt{6}$.
答:改造后的坡長AE為8$\sqrt{6}$m.
點評 本題考查了解直角三角形的應用,解答本題的關鍵是根據所給角構造直角三角形,利用三角函數的知識求解.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:初中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | B. | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | C. | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 在如圖的地板行走,隨意停下來時,站在黑色地板上的概率是( )
在如圖的地板行走,隨意停下來時,站在黑色地板上的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com